|
1 ソフト:小学校算数科5年「体積」導入・発展教材ソフト
(1)「体積」導入教材ソフト
① 内 容
サイズ:838 KBytes ファイル名:taiseki-intro.exe 作成者:Marche 種別:フリーソフト
確認済動作環境:WindowsVista,Windows 10
② 概 要
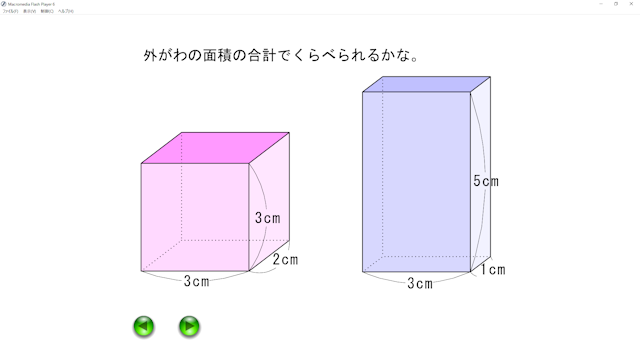
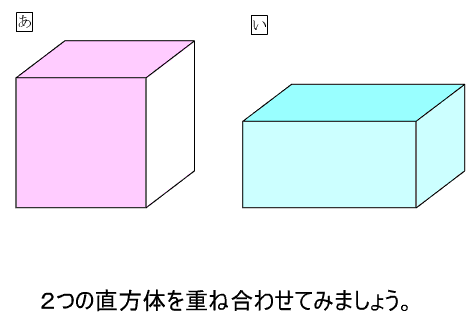
単元「体積」の導入場面の授業で,直方体と立方体の大きさくらべ問題を提示できます。
直接比較が難しい立体の大きさくらべを,動画でシミュレーションできます。
途中には,面積の学習内容を振り返ることができるようになっています。
面積の学習を基にしながら,体積の意味について話し合い,体積の意味やその測定の意味を考えることをねらいとした教材ソフトです。
(2)「体積」発展教材ソフト
① 内 容
サイズ:834 KBytes ファイル名:taiseki-kufuu.exe 作成者:Marche 種別:フリーソフト
確認済動作環境:WindowsVista,Windows 10
② 概 要
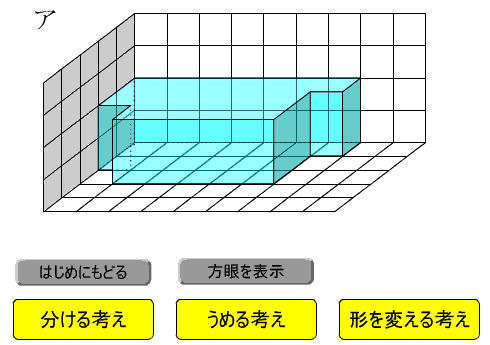
単元「体積」の発展の授業で,直方体と立方体の複合図形についての求積問題を提示する教材ソフトです。
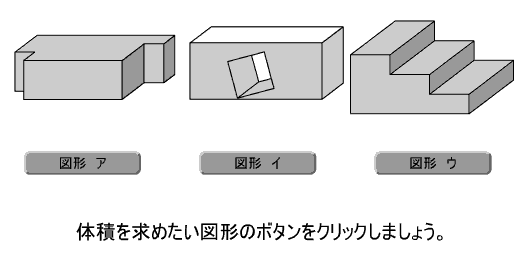
問題は3問です。3種類の立体図形の求積問題を提示できます。
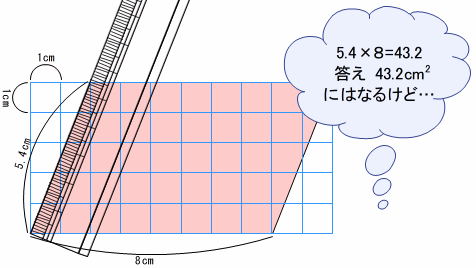
問題解決のアイデアとして,「分ける考え」「うめる考え」「形を変える考え」を動画でシミュレーションできます。
立体図形の背景に3次元の方眼を提示できるようにしています。
立体の奥行きや大きさの感覚がつかみやすくなっています。また,立体の長さや含まれる単位立方体の個数が視覚的に分かりやすくなっています。

2 単元の概要と指導のねらい
学習指導要領では,指導内容は以下のように示されています。
〔B 量と測定〕B(2)体積の単位と測定
(2)体積について単位と測定の意味を理解し,体積を計算によって求めることができるようにする。
ア 体積の単位(立方センチメートル(cm3),立方メートル(m3))について知ること。
イ 立方体及び直方体の体積の求め方を考えること。
文部科学省小学校学習指導要領解説算数編平成20年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf
単元「体積」では,体積の単位や測定の意味を理解し,体積を求めることができるようにすることがねらいです。
立体の体積も,面積などと同じように,単位の大きさを決めるとその幾つ分として数値化してとらえることができるようにします。
また,図形を決定付ける辺の長さに着目し,測定した長さの数値を基に計算で求められることが分かるようにします。
3 指導のポイント
(1)直接比較と普遍単位による測定の活動を構成する
量と測定領域の指導では,一般に,直接比較,間接比較,任意単位による測定,普遍単位による測定という学習活動を設定します。
それらを通して,量の意味や測定の単位,測定の仕方が理解できるようにします。
しかし,体積の場合は,それらの4つの活動を構成することは難しい面があります。
小さな箱と大きな箱の比較であれば,小さな箱を大きな箱に入れて直接比較はできます。
これを手がかりに,大きさ比べのイメージをつくることが考えられます。
直接包含できない立体の場合,直方体と立方体の直接比較を頭の中で思考しながら試して比べる思考実験を必要とします。
そこで,本「体積」導入教材ソフトを活用すれば,直方体と立方体の大きさくらべを,動画でシミュレーションできます。
透過した立体が,なめらかに動いて重なり,大きさを比較できます。その様子を視覚的に確かめることができます。
単元「体積」では,次のような活動を通して,児童の気付きや理解を促します。
- 立方体と直方体を重ねて比べる 【シミュレーションによる直接比較】
- 【間接比較】及び【任意単位による測定】は省きます。
- 1辺が1cmの立方体が何個分あるかで比べる【普遍単位による測定】
3の1辺が1cmの立方体が何個分あるかで比べる活動は,一人一人の児童に体験させる必要があります。
体積の意味を,理解するのに大切な活動です。
第6学年で,角柱と円柱の体積を求める際,底面積に高さをかけても体積は求められないと考える児童がいる場合があります。
底面積は面であり体積はないというのが理由です。
したがって,本単元で単位立方体の数で体積を表す体積の意味が,実感をもって理解できるようにすることが大切です。
(2)体積の単位を面積の単位から類推できるようにする
大きさくらべのための適切な普遍単位を考え話し合う場面を設定するようにします。
第4学年で,面積の適切な単位として1cm2の正方形を使うよさを学んでいます。
その学習から類推して,体積の単位を考えるようにします。
その際,単位は同種の量である必要があることを確認します。
体積の単位は,体積をもつ立体図形である必要があります。平面ではないことを十分話し合います。
さらに,空間を隙間なく埋め尽くせる立体図形が適当であることを確かめます。
その上で,立体図形としては一辺の長さでその大きさが決まる立方体が便利で,その一辺の長さが1cm や1m のように長さの単位の大きさであるものが都合がよいことなどについて話し合い,見いだせるようにします。
(3)公式化では,体積は,長さの数値の計算だけで求められるよさに気付くようにする
直方体や立方体の体積は,それぞれの辺の長さの数値が分かりさえすれば,それらの積で簡単に求められます。
長ささえ分かればよく,思考がとても楽になります。
これが算数・数学のよさのひとつであり,公式のよさでもあります。
体積は,縦,横,高さの長さの数値のみに依存しています。
それらが分かれば,体積を容易に求められます。
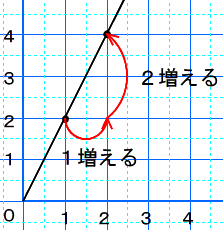
長さの数値と体積に関数関係があることがよさの秘密です。
児童には,このように考えられるよさに気付くようにします。
| 【指導のねらい】単元「体積」では,体積の単位や測定の意味を理解し,体積を求められるようにすることがねらいです。
【ポイント】 (1)直接比較と普遍単位による測定の活動を構成する (2)体積の単位を面積の単位から類推できるようにする (3)公式化では,体積は,長さの数値の計算だけで求められるよさに気付くようにする |