数学的な見方・考え方「数量関係・関数」第６学年「比例」実践例

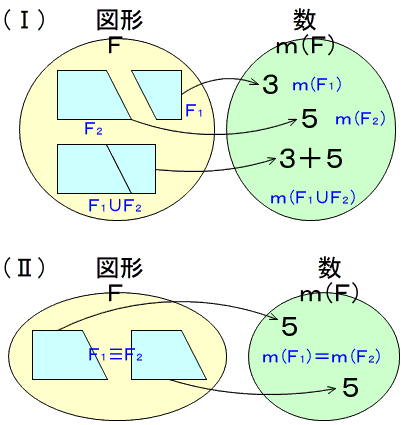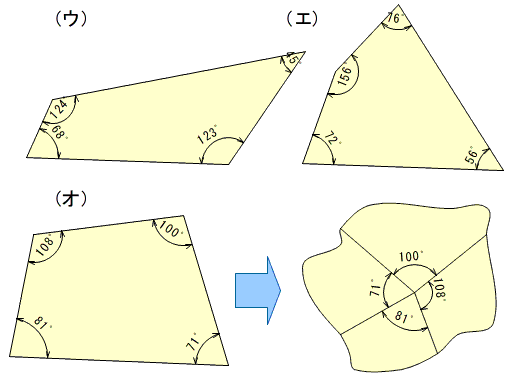
新学習指導要領の見方・考え方の具体例として，算数科「数量関係」領域の指導では，数学的な見方・考え方の指導はどのようにすればよいのでしょうか。

「数量関係」領域の指導例として，「関数」第６学年「比例」の指導では，以下の３つの活動の設定と数学的な見方・考え方の育成が考えられます。
【伴って変わる二つの数量に着目する活動】
・　数学的な見方： 一方の数量は，他のどんな数量によって決まるか，依存する関係の数量に着目する。
・　数学的な考え方： 決まれば決まるのかどうか考える。
【伴って変わる二つの数量の関係に着目する活動】
・　数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。
・　数学的な考え方：特徴や傾向を見いだすために，関係を，言葉，数，式，表，グラフに表すことを考える。
【伴って変わる二つの数量の関係をみつけ話し合う活動】
・　数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。表の二つの数量の商やグラフの傾き，式のきまった数に着目する。
・　数学的な考え方：表に現れる二つの数量の商やグラフの傾き，式のきまった数を根拠にして，演繹的にきまった数を考え，比例関係を考える。それぞれの活動で，数学的な見方・考え方が問題解決につながるようにします。
また，表やグラフはかくことで終わりではなく，かいた表やグラフを使って，きまりを見つけることができることを確かめることが重要です。
※本指導内容「比例の関係」は，平成32年度より全面実施される新学習指導要領では，上学年に新設された「C変化と関係 」領域に位置付けられます。※追記平成30年4月26日








１　算数科の見方・考え方

新学習指導要領では見方・考え方が明示されました。算数科・数学科の特質に応じた見方・考え方は，数学的な見方・考え方です。
「数学的な見方・考え方」は，算数の学習において，どのような視点で物事を捉え，どのような考え方で思考をしていくのかという，物事の特徴や本質を捉える視点や，思考の進め方や方向性を意味します。

数学的な見方・考え方
・　事象を数量や図形及びそれらの関係などに着目して捉え，根拠を基に筋道を立てて考え，統合的・発展的に考えること
数学的な見方
・　事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
数学的な考え方
・　目的に応じて数，式，図，表，グラフ等を活用しつつ，根拠を基に筋道を立てて考え，問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら，統合的・発展的に考えること

小学校算数科の数学的な見方・考え方の例が，下記のように示されています。

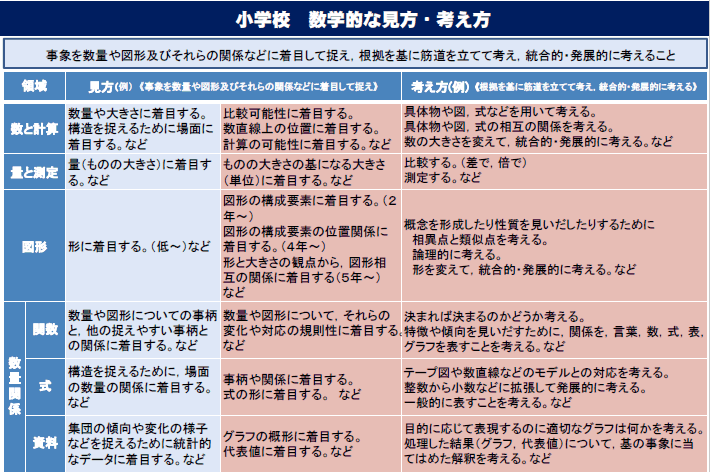
[1]文部科学省　教育課程部会算数・数学ワーキンググループ（第８回）配付資料参考資料２p5「数学的な見方・考え方」平成２８年５月２４日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf（参照2017/05/14）

２　数学的な見方・考え方の具体例

（１）「数量関係」領域「関数」の数学的な見方・考え方

「量と測定」領域「関数」の数学的な見方・考え方は，次のようです。
数学的な見方
・　数量や図形についての事柄と，他の捉えやすい事柄との関係に着目する。など
・　数量や図形について，それらの変化や対応の規則性に着目する。など
数学的な考え方
・　決まれば決まるのかどうか考える。
・　特徴や傾向を見いだすために，関係を，言葉，数，式，表， グラフを表すことを考える。など

【注意】本単元の指導内容である「比例の関係」は，平成３２年度より全面実施される新学習指導要領では，上学年に新設された「C変化と関係 」領域に位置付けられます。 現行の「数量関係」領域における関数の考えの育成については，新学習指導要領では新規に「変化と関係」領域を上学年に設定し，そこに位置付けられます。「伴って変わる数量の関係」，「比例・反比例」の指導内容は，「Ｃ 変化と関係」に含まれます。 具体的な「思考力，判断力，表現力等」の指導内容は，次のようです。 「伴って変わる二つの数量を見いだして，それらの関係に着目し，目的に応じて表や式，グラフを用いてそれらの関係を表現して，変化や対応の特徴を見いだすとともに，それらを日常生活に生かすこと。」 ※追記平成30年4月26日 五つの領域で構成された算数科の内容

（２）第６学年「比例」の数学的な見方・考え方

第６学年「数量関係」領域「比例」の指導では，これまでの数量関係についての見方をまとめるために，伴って変わる二つの数量の中から特に比例の関係を中心に考察し，関数の考えを伸ばすようにします。

① 　関数の考え

関数の考えとは，数量や図形について，それらの変化や対応の規則性に着目して問題を解決する考えです。
関数の考えを生かすために，関数の考えの数学的見方・考え方を生かして，見いだした変化や対応の規則性を，様々な問題の解決に活用し，その思考過程や結果を表現したり，説明したりすることが大切です。

②　比例の意味

・　二つの数量Ａ，Ｂの一方の量が２倍，３倍，４倍，…と変化するのに伴って，他方の数量も２倍，３倍，４倍，…と変化する。一方が，\(\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dots \) と変化するのに伴って，他方も，\(\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dots \) と変化する。
・　一般的にして，二つの数量の一方がｍ倍になれば，それと対応する他方の数量はｍ倍になる。
・　二つの数量の対応する値の商に着目すると，それがどこも一定になる。

③　「比例」の数学的な見方・考え方

数学的な見方
・　一方の数量は，他のどんな数量によって決まるか，依存する関係の数量に着目する。
・　伴って変わる二つの数量の 変化や対応の規則性に着目する。
数学的な考え方
・　決まれば決まるのかどうか考える。
・　特徴や傾向を見いだすために，関係を，言葉，数，式，表， グラフを表すことを考える。
・　約束した比例の意味に基づいて，伴って変わる二つの数量の関係を比例かどうか考える。
・　表に現れる二つの数量の商やグラフの傾き，式の決まった数から，きまった数を考える。
・　関数の考えを生かして，変化や対応の規則性に着目して問題の解決を考える。

３　指導の実際

（１）既習内容

児童は，第５学年までに，伴って変わる二つの数量の関係については，その対応や変化の仕方の特徴について，表などを用いて調べることを中心に学習しています。
特に，第５学年では，簡単な場合について，比例の関係を理解してきています。
長方形の横の長さと面積の変わり方を表にかいて調べたり，それらの関係を表や式に表したりしています。
横の長さが２倍，３倍，４倍，…と変化するのに伴って，面積も２倍，３倍，４倍，…と変化すること。そしてこのような関係にあることから面積は横の長さに比例することを学習しています。
実践例は，本単元１６時間中の第８時，伴って変わる数量の比例関係の判断をする学習場面です。

この学習までに既習内容として，
1.　伴って変わる２つの量\(x\)，\(y\)があって，\(x\)の値が２倍，３倍，…になると，\(y\)の値も２倍，３倍，…になるとき，\(y\)は\(x\)に比例します。
2.　比例する２つの量の対応する値の関係
・　比例する２つの量\(x\)，\(y\)では，「\(x\)の値」×「きまった数」＝「\(y\)の値」になっています。
・　対応する値の商がきまった数になります。「\(y\)の値」÷「\(x\)の値」＝「きまった数」　きまった数は，\(x\)の値が１のときの\(y\)の値
3.　比例の関係を表す式
・　\(y\)＝「きまった数」×\(x\)
4.　比例のグラフの特徴
・　比例する関係を表すグラフは直線で，横軸と縦軸の交わる点の通ります。
以上の内容を学んでいます。

（２）学習活動

【伴って変わる二つの数量に着目する活動】
数学的な見方： 一方の数量は，他のどんな数量によって決まるか，依存する関係の数量に着目する。
数学的な考え方： 決まれば決まるのかどうか考える。
単元の導入では，花だんの広さくらべです。

【活動１】「次の図を見て，ともなって変わる２つの量をみつけましょう。」

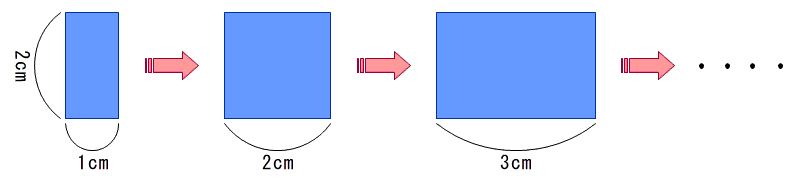
縦２ｃｍの長方形の横の長さが変わるとき，ともなって変わるのは，
Ｃ：長方形の横の長さと面積が，ともなって変わります。
Ｃ：長方形の縦の長さは変わりません。
Ｃ：長方形の横の長さが増えると面積が増えます。
このとき，長方形の横の長さと面積の関係ばかりでなく，対角線との関係など伴なって変化する数量を取り上げて，伴なって変わる数量を見いだす数学的な見方を育てることが大切です。

【伴って変わる二つの数量の関係に着目する活動】
数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。
数学的な考え方：特徴や傾向を見いだすために，関係を，言葉，数，式，表， グラフを表すことを考える。
【活動２】「その２つの量が，どのような関係にあるかを表，式，グラフを使って調べましょう。長方形の横の長さを\(x\)ｃｍ面積を\(y\)ｃｍ^２として，\(x\)と\(y\)がどのような関係にあるかを調べましょう」
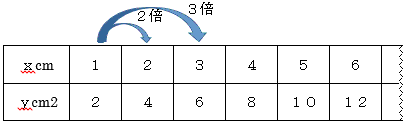Ｃ：表に書いて考えました。\(x\)が２倍，３倍，…になると\(y\)も２倍，３倍，…になります。だからは\(y\)は\(x\)に比例します。
【演繹的な考え方】既習内容１　比例の意味を根拠
Ｃ：ことばの式をもとにして，\(x\)と\(y\)の関係を式に表すました。
「面積」＝２×「長方形の横の長さ」
決まった数が２になるので，\(y=2 \times x\) となります。だから，\(y\)は\(x\)に比例します。
【演繹的な考え方】既習内容３　比例の関係を表す式を根拠
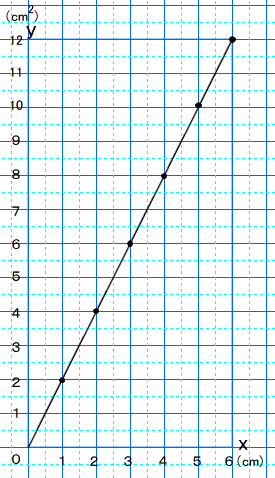Ｃ：表からグラフをかきました。１つずつ方眼紙に点を取って順につなぐと，横軸と縦軸の交わる点を通る直線になります。だから，\(y\)は\(x\)に比例します。
【演繹的な考え方】既習内容４　比例のグラフの特徴を根拠

【伴って変わる二つの数量の関係をみつけ話し合う活動】
数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。表の二つの数量の商やグラフの傾き，式のきまった数に着目する。
数学的な考え方：表に現れる二つの数量の商やグラフの傾き，式のきまった数を根拠にして，演繹的にきまった数を考え，比例関係を考える。

【活動２】「１で求めた\(y=2 \times x\)の式で，決まった数が２になるわけを表やグラフを使って説明してみましょう。」
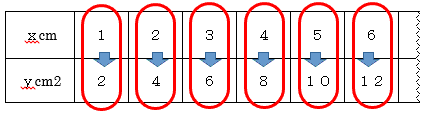表にまとめて、表の数値を横に調べると，変化の仕方が分かります。このことから比例の意味に基づいて判断できます。
表の数値を縦に調べると，\(x\)と\(y\)のきまりが分かります。
目的は決まりを見つけることです。表をかいて終わりではなく，きまった数を見つけることが大切です。
グラフではグラフの特徴から比例の判断ができます。
グラフにおいても，グラフを描くことが目的ではなく，グラフを使って決まった数を見つけることが大切です。
Ｃ：表を縦にみると，どの対応する値の商もきまった数２になるからです。
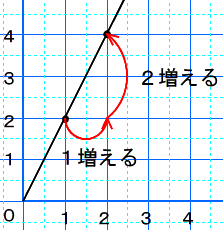
Ｃ：グラフを見ると，\(x\)の値が１増えると\(y\)の値が２増えているからです。

（５）学習のまとめと振り返り

まとめでは，
【伴って変わる二つの数量に着目する活動】
・　数学的な見方： 一方の数量は，他のどんな数量によって決まるか，依存する関係の数量に着目する。
・　数学的な考え方： 決まれば決まるのかどうか考える。
【伴って変わる二つの数量の関係に着目する活動】
・　数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。
・　数学的な考え方：特徴や傾向を見いだすために，関係を，言葉，数，式，表， グラフを表すことを考える。
【伴って変わる二つの数量の関係をみつけ話し合う活動】
・　数学的な見方： 伴って変わる二つの数量の 変化や対応の規則性に着目する。表の二つの数量の商やグラフの傾き，式のきまった数に着目する。
・　数学的な考え方：表に現れる二つの数量の商やグラフの傾き，式のきまった数を根拠にして，演繹的にきまった数を考え，比例関係を考える。

以上について，数学的な見方・考え方が問題解決につながったことをまとめ振り返られるようにします。
また，表やグラフは，かくことで終わりではなく，かいた表やグラフを使って，きまりを見つけることができることを確かめることが重要です。

既習の以下の内容についても，確かめることができたことを振り返ります。
1.　伴って変わる２つの量\(x\)，\(y\)があって，\(x\)の値が２倍，３倍，…になると，\(y\)の値も２倍，３倍，…になるとき，\(y\)は\(x\)に比例します。
2.　比例する２つの量の対応する値の関係
・　比例する２つの量\(x\)，\(y\)では，「\(x\)の値」×「きまった数」＝「\(y\)の値」になっています。
・　対応する値の商がきまった数になります。「\(y\)の値」÷「\(x\)の値」＝「きまった数」　きまった数は，\(x\)の値が１のときの\(y\)の値
3.　比例の関係を表す式
・　\(y\)＝「きまった数」×\(x\)
4.　比例のグラフの特徴
・　比例する関係を表すグラフは直線で，横軸と縦軸の交わる点の通ります。

参考文献
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）
啓林館「わくわく算数６」単元「比例と反比例」平成２７年度用