- 類推して考えるが，行き詰まることがないでしょうか。よりよい類推のためには，どのような数学的な見方・考え方をするとよいのでしょうか。
- 類推的な考え方は，既習の内容との類似性に着目して新しい事柄を見いだす考え方です。それは，見通しをもつときにしばしば活用されますが，いつも正しいとは限りません。
そこで，類推対象の基本法則や性質に着目して，類推した考えを吟味すると，より精度の高い類推に近づくようになります。
例えば，平行四辺形の面積を求める場面では，次の数学的な見方・考え方をします。
① 長方形の求積公式の意味に着目する
長方形の求積公式と同じ構造の式か。長さを測り，その数値の積を求めたか。
② 面積の測定の意味に着目する
面積は，「単位正方形の何個分」で表したか。
授業前の準備として，類推対象の面積・測定・公式の意味など性質，法則または解決の方法を模造紙にまとめ視覚化するなどして意識できるようにします。
１ はじめに
小学校算数科で学ぶ数学的な考え方として，重要でしばしば用いられる考え方が類推的な考え方です。
類推的な考え方（簡易な説明）
既習の内容との類似性に着目して新しい事柄を見いだす考え方
問題を解決するため，新しい方法をつくり結果を得ようとするとき，見通しをもち筋道を立てて考えることが必要になります。その際に有効に働く考え方の一つが類推的な考え方です。
その類推的な考え方は「似ている」性質や法則，方法などを基にして方法や結果を推測します。類推，推測であるので，その考えは必ずしも正しいとはいえません。
したがって，類推的な考え方を指導する際には，類推した考えが正しいのか確かめる態度を育てることが必要です。
児童が自ら類推した考えを検討修正できるようになれば，類推的な考え方がより洗練され有効に活用できるようになります。
そこで，類推の精度を高める数学的な見方・考え方について考えます。
２ 類推の危うさ
（１）期待される考え
【問題】平行四辺形の面積を求めましょう。
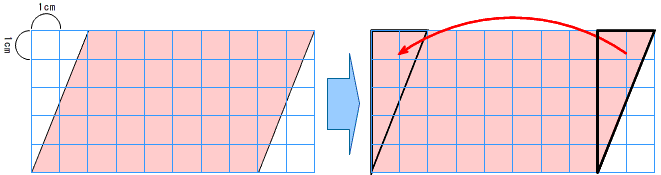
上の面積を求める場合，平行四辺形を図のように長方形などに等積変形して面積を求めます。
・ 長方形の面積=縦×横
長方形の面積を求める公式を使って，
・ ５×８=４０ 答え４０ｃｍ２
したがって，平行四辺形の面積は４０ｃｍ２と求められます。
（２）類推のつまずき
平行四辺形の面積を求めようとするとき，長方形の面積を求める公式をそのまま当てはめて考えるときがあります。
平行四辺形は，長方形に似ている。
平行四辺形の面積は，長方形の面積の求める公式と同じように考えられるのではないか。
・ 長方形の面積=縦×横
にならって
・ 平行四辺形の面積＝斜め×横
と類推します。
そして，平行四辺形の底辺と斜辺の長さを測り，その数値を使って長方形の求積公式と同じ構造で式に表します。
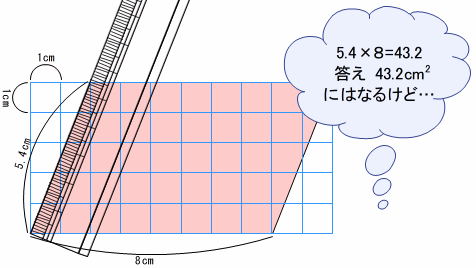
・ ５．４×８=４３．２ 答え ４３．２ｃｍ２
となるけれど…
面積は小数になりました。「平行四辺形の面積＝斜め×横」は成り立つのか不安になり行き詰まってしまいました。
３ 類推を修正する視点をもつ数学的活動
この例では，自分の考えは正しいのか，どこをどのように改善するとよいのか，児童は行き詰まり自力解決が困難な状況です。
そこで，次のような指導が考えられます。
（１）意味に着目する
まず，面積とその測定の意味，長方形の公式の意味を振り返ることが重要です。
・ 面積の意味：広さのことを面積といい，面積は，１辺が１ｃｍの正方形（単位正方形）が何個分あるかで表します。
・ 長方形の面積を求める公式：長方形の面積＝たて×横
長方形の面積は，単位正方形の数を表すたてと横の長さがそれぞれ何ｃｍあるかを測り，その数値をかけあわせて求めることができます。単位正方形の面積は，１ｃｍ２です。
（２）他の考えと比較する
児童の考えとしては，主に平行四辺形を長方形に等積変形する多様な方法が予想されます。ここでは，考えの妥当性を検討するため，以下の二つの考えを比較します。
【問題】平行四辺形の面積を求めましょう。
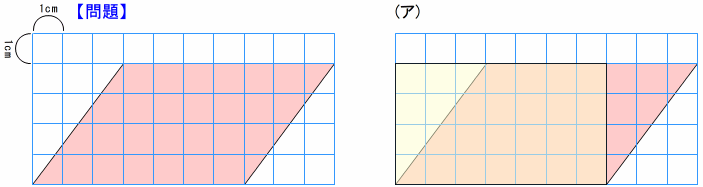方法１ 平行四辺形を，長方形に等積変形して考えた場合
図（ア）…… ８×４（４×８）＝３２ 答え ３２ｃｍ２
方法２ 長方形の面積の公式から類推して「平行四辺形の面積＝斜め×横」と考えた場合
図（ウ）…… ５×８=４０ 答え４０ｃｍ２
【参考】問題には，斜辺５ｃｍ高さ４ｃｍの平行四辺形を提示します。斜辺の長さも整数値になるようにします。ノートでの作図が容易であり，この大きさが適切です。
（３）公式と面積の意味に着目した検討
妥当性を検討する場面では，面積の意味と長方形の公式の意味に着目した数学的な見方・考え方から，類推した考えを検討します。
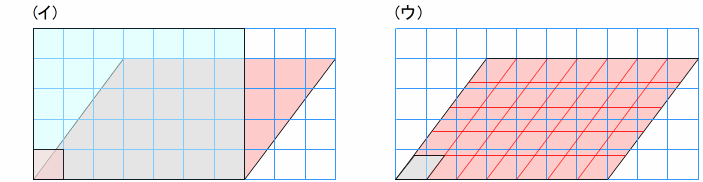長方形の求積公式の意味に着目して［方法２］を検討する
・ 長方形の求積公式：長方形の面積＝縦×横 縦と横の長さを測定した数値の積
・ 類推した式：平行四辺形の面積＝斜め×横 斜めと横の長さを測定した数値の積
類推した式が成り立つとすれば，各辺の長さを測定した数値の積を求める手続きは正しそうです。正しくは単位正方形の数を表す長さを測定しているかが検討されるべきです。それが次の視点です。
面積の測定の意味に着目して［方法２］を検討する
面積は，１辺が１ｃｍの正方形（単位正方形）が何個分あるかで表します。これが面積の意味です。
したがって，平行四辺形の面積を求めるには，平行四辺形に含まれる単位正方形（青いマス目）の数を測る必要があります。
斜め×横，５×８の式が成り立つとすると，（イ）の図のように平行四辺形の面積と青の長方形（縦５ｃｍ横８ｃｍ）の面積とが等しいことになります。この考えについて，面積の意味に基づいて妥当性を検討する話し合いが必要です。
単位正方形の数を比べると
長方形の面積：５×８=４０ 答え４０ｃｍ２
平行四辺形の面積：青のマス目の数を数えるなどして３２ｃｍ２
長方形の面積：４０ｃｍ２＞平行四辺形の面積：３２ｃｍ２
「斜め×横」で求めた数は，（ウ）のように赤のマス目の平行四辺形の数です。その数は単位正方形の数を表しません。
底辺に垂直な高さの数（青のマス目）を使うと，単位正方形の数を求められます。測定しているものは何か，数えているものは何かを再度確かめる話し合いが必要です。
（４）面積の意味に着目した確かめ
つまずきの例として，単位正方形と単位となる平行四辺形の面積が同じと考える場合があります。また，平行四辺形の面積と斜辺と底辺の長さでできる長方形の面積とが同じと考える場合もあります。それらのつまずきに対しては，面積の意味に着目した確かめの問題提起が有効と考えられます。必要に応じて斜辺を極端に傾けた平行四辺形の面積を提示して，つまずきの解消を図るようにします。
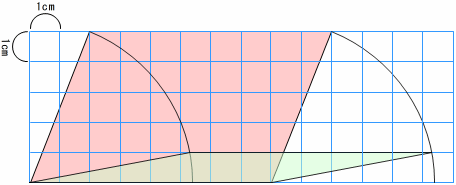面積は，本来は下のようになります。
ア（赤）平行四辺形の面積 ８×５．４=４３．２ 答え ４３．２ｃｍ２
イ（緑）平行四辺形の面積 ８×１＝８ 答え ８ｃｍ２
ところが，「 平行四辺形の面積＝斜め×横」が成り立つとすると，
ウ（赤・緑）平行四辺形の面積 ８×５．４=４３．２ 答え ４３．２ｃｍ２
ウのように面積を求める式が同じになり，赤と緑の平行四辺形の面積が等しいことになります。しかし，緑の平行四辺形の面積が４３．２ｃｍ２あるように見えないことから，単位正方形のマス目を数えます。
すると，多く見積もっても１３ｃｍ２を上回りません。これは，計算結果に矛盾します。
したがって，「長方形の面積＝縦×横」にならって平行四辺形の公式を「平行四辺形の面積＝斜め×横」と類推しましたが，そのようには仮定できないということです。
面積の意味に着目した数学的な見方・考え方を働かせる
ここで，面積の意味に着目した数学的な見方・考え方を働かせます。
そもそも面積を求めるために測定していたのは単位正方形の数でした。単位正方形は横には８個並びます。しかし，斜辺には隙間なく並べられません。このことは斜辺の長さは単位正方形の数を数えることに使えないことを意味します。
したがって，平行四辺形のどこの直線の長さに単位正方形の数が表れるかを検討する必要があります。
単位正方形の四つの角は直角です。そのため単位正方形の数は直交する直線に表れます。面積の測定に必要な長さは，平行四辺形に含まれる直行する直線です。その直線を見つけられれば，それらの数値の積で面積が求められます。このことから，底辺と高さの用語が導入されます。
確かな理解のためには，測定しているものは何か，数えているものは何かを再度確かめる話し合いが必要です。
４ 平行四辺形の求積での数学的な見方・考え方の働かせ方
（１）意味に着目して類推を吟味する
【結論】「類推のつまずき例」のような考えがあるときは，類推対象の面積・測定・公式の意味を基にして，類推した考えを吟味する話し合いをします。
例えば，平行四辺形の求積で，長方形の求積公式にならって「平行四辺形の面積＝斜め×横」と考えたときは，次の①と②の数学的な見方・考え方から吟味します。
① 長方形の求積公式の意味に着目する
・ 長方形の求積公式と同じ構造の式か。単位正方形の数を表す長さを測り，その数値の積を求めたか。
② 面積の測定の意味に着目する
・ 面積は，「単位正方形の何個分」で表したか。
類推的な考え方は，既習の内容との類似性に着目して新しい事柄を見いだす考え方です。それは，見通しをもつときにしばしば活用されますが，類推した考えがいつも正しいとは限りません。
そこで，対象の基本法則や性質に着目した数学的な見方・考え方で，類推した考えを吟味すると，類推による考えがより洗練されるようになります。
（２）期待される数学的な見方・考え方の働かせ方
① 類推の準備
長方形や正方形の面積・測定・公式の意味など，関連する既習事項を意識できるようにします。すなわち，類推対象の基本法則や性質に着目した数学的な見方・考え方を働かせながら，類推的な考え方を働かせることができるようにします。
類推は既習内容の類似性に着目するのであるから，児童が関連する既習の意味や性質，法則，解決の方法の要点をつかんで学習問題を考えられるようにします。面積・測定・公式の意味など，前時，単元，系統，領域レベルで関連する必要な内容を模造紙にまとめ視覚化するなどして随時活用できるようにします。
② 意味に着目して類推する
【結論】平行四辺形の面積を求めようとするときは，長方形の面積・測定・公式の意味に着目して，それらから類推して求積方法を考えることができるようにします。
より一般的に言えば，類推する対象の基本法則や性質に着目した数学的な見方・考え方を働かせながら，類推的な考え方を働かせると，より精度の高い考えになります。「類推する対象の基本法則や性質に着目」することについては，数学の内容に関係した数学的な考え方の「基本的性質の考え」に当たります。
例えば，平行四辺形の面積を求めようとするときは，次の点などに着目して考えるようにします。
① 面積やその測定の意味
・ 面積を「単位正方形の何個分」で表そうとしているか。
・ 単位正方形を隙間なく並べて，その数を正しく測定しようとしているか。
② 長方形の求積公式の意味
・ 長方形の求積公式と同じ構造の式をつくろうとしているか。
・ 単位正方形の数を表す長さを測り，その数値の積を求めようとしているか。
③ 長方形と平行四辺形の共通点と相違点
・ 平行四辺形と似た図形は長方形であり，平行四辺形を長方形とつなごうとしているか。
・ 長方形の求積公式を使うために，平行四辺形を長方形に変形しようとしているか。
授業前の準備として，類推対象の面積・測定・公式の意味など性質，法則または解決の方法を模造紙にまとめ視覚化します。それにより，それらをいつでも参照でき常に意識できるようにします。
【参考】平行四辺形の面積は，三角関数を使うと底辺aと斜辺b，それらのなす角θが分かれば求められます。
・ 平行四辺形の面積＝absinθ
その場合でも結果として「底辺×高さ」を求めることになります。
参考文献 片桐重男 数学的な考え方とその指導第１巻「数学的な考え方の具現化と指導」明治図書２００４年
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）
啓林館 わくわく算数５平成２７年度版
