- 小学校算数科で育成する数学的な考え方の「演繹的な考え方」とは，どのような考え方なのでしょうか。
- すでに正しいことが明らかになっている事柄を基にして別の新しい事柄が正しいことを説明していく考え方です。
いつでもいえるということを主張するためにすでに分かっていることを基にして，その正しいことを説明しようとするものです。
問題解決の方法や結果が正しいことをきちんと示すためには，筋道を立てて考えることが求められます。演繹的な考え方は，根拠を明らかにしながら，筋道を立てて考える代表的な考え方です。
１ はじめに
小学校算数科で学ぶ数学的な考え方として，筋道を立てた論理的な思考の代表が演繹的な考え方です。
演繹的な考え方
「すでに正しいことが明らかになっている事柄を基にして別の新しい事柄が正しいことを説明していく」考え方
問題を解決するため，新しい方法をつくり結果を得ようとするとき，見通しをもち筋道を立てて考えることが必要になります。
見通しをもつには，帰納的な考え方や類推的な考え方を用いることがあります。
・ 見通し：「解決のための方法」についての見通しと「結果」についての見通し
・ 帰納的な考え：いくつかの具体例を調べて共通性を見付ける考え方
・ 類推的な考え：既習の内容との類似性に着目して新しい事柄を見いだす考え方
見通しをもつことは，問題の解決を適切にまた合理的に進めていく上で重要です。
問題解決の方法や結果が正しいことをきちんと示すためには，筋道を立てて考えることが求められます。
根拠を明らかにしながら，一歩ずつ進めて筋道を立てて考える代表的な考え方が，演繹的な考え方です。
なお，学習指導要領解説*2では「演繹的な考え」と表記されていますが，筆者は「演繹的な考え方」と表記しています。
「考え」 は考えた内容や結論をいい，「考え方」 は考える方法や思考の順序をいいます。したがって，演繹的な考え方は，考える方法であることから，「考え方」と表記します。
数学的な考え方の数学的な意味は，片桐重男著「数学的考え方の具体化と指導」*1によります。
簡便な説明では，「文部科学省小学校学習指導要領解説 算数編」*2で解説されている表記によります。
※１９８８年出版の前著「数学的考え方の具体化」片桐重男著は，理論的な解説が充実し，筆者が信頼を寄せる名著です。絶版だったのですが，読みやすく編集され，新版が出版されました。専門的に学びたい方には座右の書にしたい著書の一つです。
２ 演繹的な考え方と評価
演繹的な考え方
いつでもいえるということを主張するためにすでに分かっていることを基にして，その正しいことを説明しようとする考え方である。
人が考えている状況を直接捉えて評価することは困難です。そこで，思考の結果として現れるものをもって評価する必要があります。以下では，説明に使用する言葉等を中心にして，演繹的な考え方をしているのかどうかを評価します。
また，演繹的な考え方では，正しいことが分かっていることを基に説明します。そのため，基にするものを明確にする必要があります。
以下に示す「根拠」とは，演繹的な考え方で説明するときに基にする，既に分かっていること，正しいことが明らかになっていることのことです。
３ 事例１ 四角形の内角の和
三角形の三つの角の大きさの和が１８０゜であることを基に，四角形が三角形二つに分割されることから１８０゜の２倍であると考えるのは，演繹的な考え方です。
根拠
○ 四角形の内角の和を求める前時までに，「三角形の３つの角の大きさの和は１８０°である」が正しいことが明らかになっています。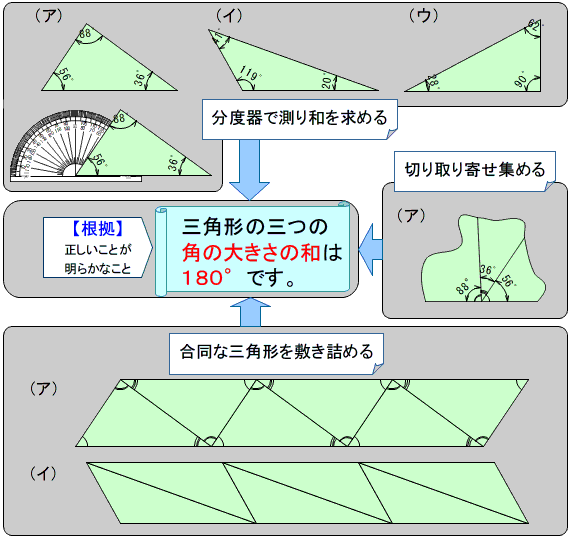
演繹的な説明
【問題】「四角形の４つの角の大きさの和が１８０°になることを説明しましょう。」
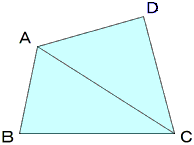【２つの三角形に分ける考え】
四角形を対角線で２つの三角形に分けます。
三角形の３つの角の大きさの和は，１８０°です。
四角形の４つの角の大きさの和は，三角形２つ分の角の大きさの和と同じになるから
・ １８０°×２＝３６０° 答え３６０°
【４つの三角形に分ける考え】
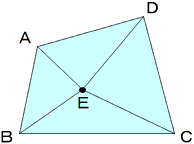
四角形の中に点Ｅをとり，四角形を４つの三角形に分けます。
１つの三角形の角の大きさの和は１８０°なので，三角形の４つ分の角の大きさの和は，
・ １８０°×４＝７２０°
点Ｅの周りの角の大きさは３６０°だから，これをひいて，
・ ７２０°－３６０°＝３６０° 答え３６０°
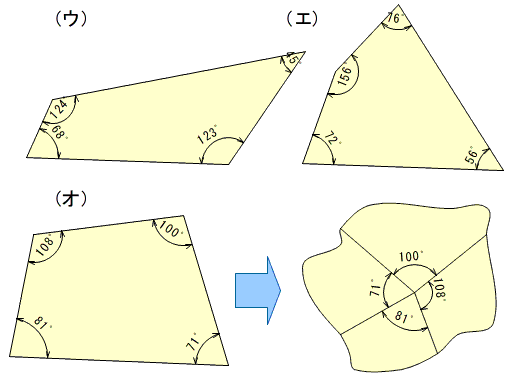
このように，三角形の３つの角の大きさの和が１８０°であることを基にして，四角形の４つの角の大きさの和が３６０°になることを説明することができます。
これが演繹的な考え方です。
４ 事例２ たし算（合併）
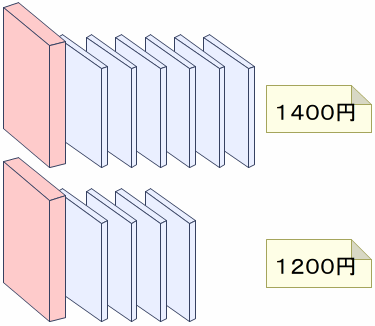
第１学年「たしざん（１）」では，加法が用いられる場合として，合併の場合を指導します。
同時に存在する二つの数量を合わせた大きさを求める場合です。
たしざんの学習では，演算が加法であることを，ブロックを両手で集める操作となったときと約束します。
したがって，児童が，「ブロックをあつめるのでたしざんです。」と考えて説明するのは演繹的な考え方です。
根拠
〇 ブロックを両手で集める操作となったとき，演算は加法であることを確かめています。
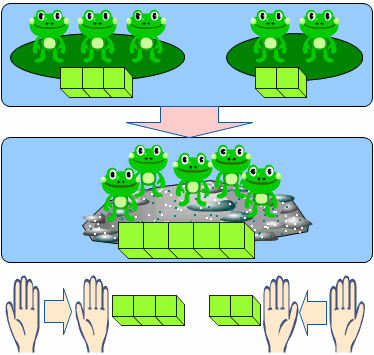
演繹的な説明
【問題】「ぜんぶで なんさつですか。」
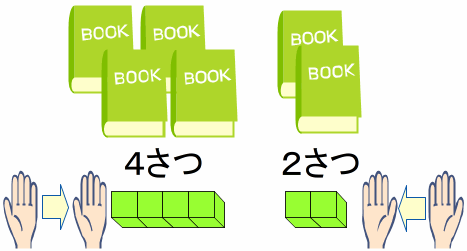
「ブロックを あつめるから たしざんです。」
しき ４＋２＝６ こたえ ６さつ
はじめにある数量に，追加したり，それから増加したりしたときの大きさを求める場合（増加）でも，ブロックを集めた操作の結果は同じになります。
このことから，たし算の適用場面を広げて，合併と増加はたし算であると理解できるようにします。
５ 事例３ 数の大きさくらべ
第１学年「１００までのかず」では，十進位取り記数法の考え方にしたがって，１００までの数の構成，順序，系列，大小について理解できるようにします。また数表や数直線を活用することで，数の連続性についても気付くようにします。
数の大小の比較では，十の位の数の大きさをくらべたり，同じ場合は一の位の数の大きさでくらべたりして数の大小を説明するのは演繹的な考え方です。
根拠
〇 前時までに，１から１００までの数を順序よくかき，１００までの数の順序が分かっています。
表を使って特定の数の上下左右の１小さい１０大きいなどの大きさや順序の関係も確かめています。
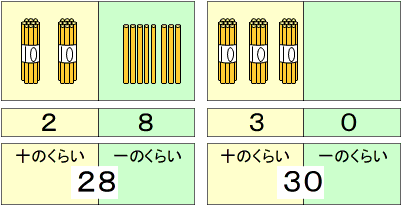
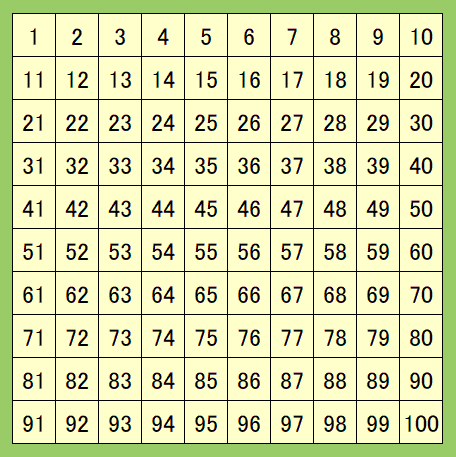〇 十のくらい，一のくらいの意味と，１０の束が８つとばらが２つで８２など，数の大きさを確かめています。
演繹的な説明
【問題】「てんすうを くらべましょう。」
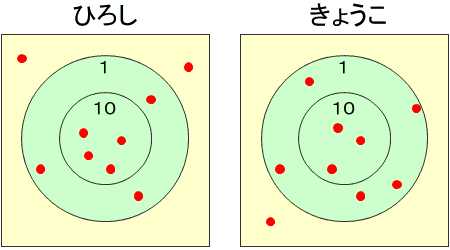ひろし １０てんが ４こと １てんが ３こ だから ４３てん
きょうこ １０てんが ３こと １てんが ５こ だから ３…
きょうこ 十のくらいが ３より ４のほうが 大きいので，ひろしさんの てんすうの ほうが 大きいです。
演繹的な考え方は，低学年から指導できる考え方です。
「どうしてそう考えたのか。」「わけは…だからです。」等，理由を説明する態度を身に付けられるようにすることが大切です。
６ まとめ
小学校算数科で育成する数学的な考え方の「演繹的な考え方」とは，すでに正しいことが明らかになっている事柄を基にして別の新しい事柄が正しいことを説明していく考え方です。
いつでもいえるということを主張するために，既に分かっていることを基にして，その正しいことを説明しようとするものです。
問題解決の方法や結果が正しいことをきちんと示すためには，筋道を立てて考えることが求められます。演繹的な考え方は，根拠を明らかにしながら，筋道を立てて考える代表的な考え方です。
参考文献 片桐重男 数学的な考え方とその指導第１巻「数学的な考え方の具現化と指導」明治図書２００４年
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）
啓林館 わくわく算数５平成２７年度版
