同じ数量に着目する数学的な見方・考え方

新学習指導要領の見方・考え方の具体例として，考えを表現し伝え合う学習活動での数学的な見方・考え方の指導はどのような事例があるでしょうか。

第５学年の同じ量に着目して問題解決する，次のような事例があります。
数学的な見方…複雑な問題をできるだけ単純化して解決する方法として，同じ数量に着目すること
数学的な考え方…「相殺の考え」「置き換えの考え」
実践では，問題の数量にうち，同じ数量に着目して，相殺や置き換えの考えを使って単純化して問題解決を考えます。








１　考えを表現し伝え合うなどの学習活動

学習指導要領では，考えを表現し伝え合うなどの学習活動について
「思考力，判断力，表現力等を育成するため，各学年の内容の指導に当たっては，言葉，数，式，図，表，グラフを用いて考えたり，説明したり，互いに自分の考えを表現し伝え合ったりするなどの学習活動を積極的に取り入れるようにすること。(小学校学習指導要領 第３節算数 指導計画の作成と内容の取扱い ２内容の取扱いについての配慮事項)」のようにその必要性を述べています。
そのような学習活動の中で育成する数学的な思考力，判断力，表現力等は，学力の中心的な要素となる一つであり，合理的，論理的に考えを進める力となるものです。また，児童が相互に知的なコミュニケーションを図るために重要な役割を果たすものです。

このように，数学的な思考力，判断力，表現力等を育成するためには，言葉，数，式，図，表，グラフを用いて考えたり，説明したり，互いに自分の考えを表現し伝え合ったりするなどの学習活動を積極的に取り入れていく必要があります。以下では，線分図などを用いて表現したり話し合ったりする活動を通して，考え方のよさなどに気付くようにすることが大切です。

２　同じ数量に着目する数学的な見方・考え方

複雑な問題をできるだけ単純化して解決する方法として，二つの数量の中から共通のものを差し引いて考える「相殺の考え」や，ある数量をそれと同等の他の数量に置き換えて考える「置き換えの考え」があります。
「相殺の考え」や「置き換えの考え」は，合理的な問題解決の数学的な見方・考え方として工夫されたアイデアの一つです。
どちらの考えも「同じ数量」に着目する数学的な見方が問題解決の鍵となります。
指導に当たっては，児童の考えの積極的な話合いの活動を設定し，「同じ数量に」着目する数学的な見方や「相殺の考え」や「置き換えの考え」のアイデアのよさに気付くようにすることが大切です。そして，このような数学的な見方・考え方が活用できるようにすることが大切です。

３　指導の実際

数学的な見方：複雑な問題をできるだけ単純化して解決する方法として，「同じ数量に」着目する
数学的な考え方：
・　相殺の考え…二つの数量の中から共通のものを差し引いて考える考え
・　置き換えの考え…ある数量をそれと同等の他の数量に置き換えて考える考え

（１）相殺の考え

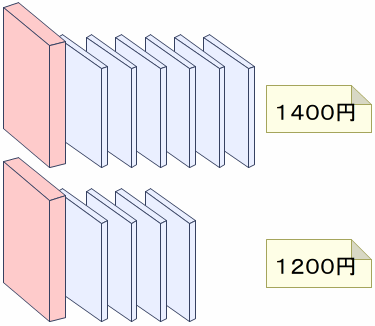
【問題】「物語の本１さつとノート６さつを買うと，１４００円になりました。物語の本1さつとノート４さつでは，１２００円になるそうです。物語の本１さつの値段は何円ですか。」
問題場面を線分図に表すと，下のようになります。
物語の本とノート４さつのねだんを差し引いて考えます。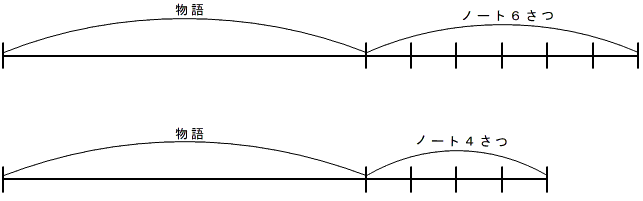
１４００－１２００＝２００…ノート２さつ分のねだん
２００÷２＝１００…ノート１さつ分のねだん
したがって，物語の本１さつのねだんは，
１４００－１００×６＝８００　答え８００円

（２）置き換えの考え

【問題】「科学の本１さつのねだんは，工作の本の２倍です。科学の本と１さつ分と工作の本１さつ分のねだんをあわせると，２４００円です。科学の本１さつと工作の本の１さつのねだんは，それぞれ何円ですか。」
問題場面を線分図に表すと，下のようになります。

科学の１さつ分のねだんを，工作の本２さつ分のねだんに置き換えて考えます。
科学の本１さつ分のねだんを，工作の本２さつ分のねだんと考えると，
工作の本３さつ分のねだんが，２４００円となります。
たがら，工作の本１さつ分のねだんは，
２４００÷３＝８００
科学の本のねだんは，
２４００－８００＝１６００　答え　科学の本１さつのねだん　１６００円，工作の本１さつのねだん　８００円

４　同じ数量に着目する数学的な見方・考え方の活用

「同じ数量に着目する数学的な見方・考え方」は，次のような場面で有効に働きます。

$$0.99999\cdots = 1 ?, \neq 1 ?$$

\(0.99999\cdots\) は，\(1\) は超えないにしても，\(1\) と等しいといえるのでしょうか。
そのことは，どのように説明できるのでしょう。

\(0.99999\cdots\) が \(1\) と等しいことには，「相殺の考え」や「置き換えの考え」を使って説明できます。
\(x=0.99999\cdots\)　とします。両辺を \(10\) 倍して，
\begin{array}{rclr}
x&=&0.99999 \cdots &\quad①\\
10x&=&9.9999 \cdots&\quad②\end{array}

\(10\) 倍した式②と元の式①の辺々を差し引きます。
\begin{array}{crcll}
&10x&=&9.99999\cdots&②\\
-&x&=&0.99999\cdots&①\\ \hline
&9x&=&9&③\\
\end{array}
これにより，循環する小数部分を消すことができます。
③の両辺を\(9\) で割ります。
$$x=1$$
となり，\(0.99999\cdots\) は，\(1\) と等しいといえます。

このように，一見難しそうな問題の場合も，相殺の考えや置き換えの考えを使うと容易に説明できることがあります。
詳しくは，別稿「0.99999… と 1 は等しいのか？」をご参照下さい。