平成２９年告示の中学校学習指導要領「数学科の目標」は，どのようなものでしょうか。

中学校数学科では，「数学的な見方・考え方を働かせ，数学的活動を通して，数学的に考える資質・能力」の育成を目指します。
・　数量や図形などについての基礎的・基本的な知識及び技能を確実に習得し，
・　これらを活用して問題を解決するために必要な数学的な思考力，判断力，表現力等を育むとともに，
・　数学のよさを知り，数学と実社会との関連についての理解を深め，数学を主体的に生活や学習に生かそうとしたり，問題解決の過程を評価・改善しようとしたりするなど，
数学的に考える資質・能力を育成することを目指します。
数学的な見方・考え方とは，
事象を，数量や図形及びそれらの関係などに着目して捉え，論理的，統合的・発展的に考えること，
数学的活動とは，
事象を数理的に捉え，数学の問題を見いだし，問題を自立的，協働的に解決する過程を遂行することです。

掲載の趣旨

平成２９年告示の学習指導要領では，資質・能力や内容などの全体像を分かりやすく見渡せるよう，枠組みが大きく見直され「学びの地図」として整理されました。
その趣旨に添い，本稿では，解説本文を次のように編集しています。
・　目標解説の内容が捉えやすいように原文を装飾
・　他教科等・他学校種の目標や解説が比較しやすように編集
具体的には，本文は原文通りで，次のように編集しています。
・　各教科等の目標の解説を共通した章立てで構成
・　学校種間の対応する内容についてリンクで移動　など
掲載の趣旨の詳細は，下のボタンより参照できます。

「掲載の趣旨」の詳細

なお，本稿は，「文部科学省ウェブサイト利用規約」（2018年3月1日に利用）に基づいて，原本を加工し作成しています。
小学校・中学校各教科等の目標の解説　「小・中学校「教科等の目標解説を縦横に読む」シリーズ」は，下のボタンより閲覧できます。

小・中学校各教科等の目標解説








中学校　数学科の目標

１　教科の目標

（１）目標の設定について

中学校数学科においては，
数量や図形などについての基礎的・基本的な知識及び技能を確実に習得し，
これらを活用して問題を解決するために必要な数学的な思考力，判断力，表現力等を育むとともに，
数学のよさを知り，数学と実社会との関連についての理解を深め，数学を主体的に生活や学習に生かそうとしたり，問題解決の過程を評価・改善しようとしたりするなど，
数学的に考える資質・能力を育成することを目指すこととした。

※ 数学科「数学のよさを知り，数学と実社会との関連」→算数科「数学のよさに気付き，算数と日常生活との関連」
※ 本項目は，他教科等にはない算数科・数学科特有の設定。
筆者拙考：本項目は，目指す方向性を明示する数学科学習指導の基本理念と考えられる。また，本項目を数学科教育の体系の中で総括目標（上位目標）と考えると，「目標の設定についての考え方」は数学科教育の目的であり，「数学科の目標」はその手段という見方もできる。

小学校算数科「目標の設定についての考え方」

（２）目標

中学校学習指導要領の数学科の目標は，次のとおりである。

※　柱書は，小学校算数科，中学校・高等学校数学科で共通。
※　平成20年中学校学習指導要領「数学」目標
「数学的活動を通して，数量や図形などに関する基礎的な概念や原理・法則についての理解を深め，数学的な表現や処理の仕方を習得し，事象を数理的に考察し表現する能力を高めるとともに，数学的活動の楽しさや数学のよさを実感し，それらを活用して考えたり判断したりしようとする態度を育てる。」
※　平成10年中学校学習指導要領「数学」目標
「数量，図形などに関する基礎的な概念や原理・法則の理解を深め，数学的な表現や処理の仕方を習得し，事象を数理的に考察する能力を高めるとともに，数学的活動の楽しさ，数学的な見方や考え方のよさを知り，それらを進んで活用する態度を育てる。」
※　平成元年中学校学習指導要領「数学」目標
「数量，図形などに関する基礎的な概念や原理・法則の理解を探め，数学的な表現や処理の仕方を習得し，事象を数理的に考察する能力を高めるとともに数学的な見方や考え方のよさを知り，それらを進んで活用する態度を育てる。」

小学校算数科「目標」

（３）目標の構成

今回の改訂では，中学校数学科の目標を，
(1)　知識及び技能，
(2)　思考力，判断力，表現力等，
(3)　学びに向かう力，人間性等
の三つの柱に基づいて示すとともに，
それら数学的に考える資質・能力全体を
「数学的な見方・考え方を働かせ，数学的活動を通して」
育成することを目指すことを柱書に示した。

すなわち，中学校数学科の目標をなす資質・能力の三つの柱は，数学的な見方・考え方と数学的活動に相互に関連をもたせながら，全体として育成されることに配慮する必要がある。

ここでは，中学校数学科の目標を，大きく六つに分けて説明する。

※ 原文では，次の六つの見出しで解説内容が構成される。
①「数学的な見方・考え方を働かせ」について
②「数学的活動を通して」について
③「数学的に考える資質・能力を育成すること」について
④「数量や図形などについての基礎的な概念や原理・法則などを理解するとともに，事象を数学化したり，数学的に解釈したり，数学的に表現・処理したりする技能を身に付けるようにする」について
⑤「数学を活用して事象を論理的に考察する力，数量や図形などの性質を見いだし
⑥「数学的活動の楽しさや数学のよさを実感して粘り強く考え，数学を生活や学習に生かそうとする態度，問題解決の過程を振り返って評価・改善しようとする態度を養う」について統合的・発展的に考察する力，数学的な表現を用いて事象を簡潔・明瞭・的確に表現する力を養う」について

小学校算数科「目標の構成」

２　柱書

（１）見方・考え方

【「数学的な見方・考え方を働かせ」について】

① 「数学的な見方・考え方」の役割・意義

中央教育審議会答申において，「見方・考え方」が，各教科等の特質に応じた物事を捉える視点や考え方として整理されたことを踏まえると，
「数学的な見方・考え方」は，数学の学習において，どのような視点で物事を捉え，どのような考え方で思考をしていくのかという，物事の特徴や本質を捉える視点や，思考の進め方や方向性を意味することと考えられる。

また，答申において，
「既に身に付けた資質・能力の三つの柱によって支えられた「見方・考え方」が，習得・活用・探究という学びの過程の中で働くことを通じて，資質・能力が更に伸ばされたり，新たな資質・能力が育まれたりし，それによって「見方・考え方」が更に豊かなものになる，という相互の関係にある」
と示されたことを踏まえ，「数学的な見方・考え方」は，数学的に考える資質・能力の三つの柱である「知識及び技能」，「思考力，判断力，表現力等」及び「学びに向かう力，人間性等」の全てに働かせるものと考えられる。

さらに，「数学的な見方・考え方」は，数学の学習の中で働かせるだけではなく，大人になって生活していくに当たっても重要な働きをするものと考えられる。数学の学びの中で鍛えられた見方・考え方を働かせながら，世の中の様々な物事を理解し思考し，よりよい社会や自らの人生を創り出していくことが期待される。

※　【英訳（仮訳）】中学校学習指導要領では，「各教科等の特質に応じた物事を捉える視点や考え方（以下「見方・考え方」という。）」を「discipline-based epistemological approaches, hereinafter referred to as “Approaches”」と訳す。見方・考え方を“Approaches”で代表している。このことを考え合わせると見方・考え方の意味がより一層捉えやすくなる。すなわち，見方・考え方は，物事を認識するときの入り方，近づき方，せまり方と言い換えることができる。
引用：文部科学省「平成29年改訂中学校学習指導要領英訳版（仮訳）」[ONLINE]https://www.mext.go.jp/content/20200227-mxt_kyoiku02-100002604_2.pdf(cf:2020.05.26)

② 「数学的な見方・考え方」の意味

「数学的な見方・考え方」のうち，
「数学的な見方」は，
「事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること」
であると考えられる。また，
「数学的な考え方」は，
「目的に応じて数，式，図，表，グラフ等を活用しつつ，論理的に考え，問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら，統合的・発展的に考えること」
であると考えられる。

※　算数科では，数学的な見方は同様。数学的な考え方は，「根拠を基に筋道を立てて考え，問題解決の過程を…」となる。

以上のことから，
「数学的な見方・考え方」は，
「事象を，数量や図形及びそれらの関係などに着目して捉え，論理的，統合的・発展的に考えること」
として整理することができる。

※　算数科では，数学的な見方・考え方は，「…に着目して捉え，根拠を基に筋道を立てて考え，統合的・発展的に考えること」となる。

③ 統合的・発展的に考える

「数学的な見方・考え方」は，数学的に考える資質・能力を支え，方向付けるものであり，数学の学習が創造的に行われるために欠かせないものである。
また，生徒一人一人が目的意識をもって問題を発見したり解決したりする際に積極的に働かせていくものである。
そのために，今回の改訂では，統合的・発展的に考えることを重視している。

なお，発展的に考えるとは，
数学を既成のものとみなしたり，固定的で確定的なものとみなしたりせず，新たな概念，原理・法則などを創造しようとすることである。
例えば，０と正の数だけでは，０より小さい数量を適切に表現することはできない。また，０と正の数の範囲で加法はいつでもできるが，減法はいつでもできるとは限らない。こうした問題を解決するために数の範囲を拡（ひろ）げることが発展的に考えることになる。

また，数の範囲を正の数と負の数にまで拡張することに対応して，四則計算の意味も，関連して広げて考えるようにすることも必要になる。既習のものと新しく生み出したものとを包括的に扱えるように意味を規定したり，処理の仕方をまとめたりすることが統合的に考えることになる。

数学の学習では，このように創造的な発展を図るとともに，創造したものをより高い，あるいは，より広い観点から統合してみられるようにすることが大切である。

④ 数学的な見方・考え方を働かせる

数学的な見方・考え方を働かせることについては，
例えば，関数領域において，「一つの数量を調べようとするとき，それと関係が深い他の数量を見いだし，それらの数量との間に成り立つ関係を明らかにし，その関係を利用する」ことが考えられる。

このような見方・考え方を働かせた活動を通して，「知識及び技能」，「思考力，判断力，表現力等」及び「学びに向かう力，人間性等」が育成される。

・　関数領域において数学的な見方・考え方を働かせる際には，未知の事象を考察するために新しい概念をつくることがあり，「知識及び技能」と関わっている。
・　また，事象を理想化したり単純化したりするなどして，数量と別の数量との間に既知の関数関係が成り立つと仮定して問題を解決するなど「思考力，判断力，表現力等」が必要となる。
・　さらに，日常の事象や社会の事象に関心をもち，事象の中に隠れた法則を見いだしたり，日常生活や社会に生かそうとしたりする科学的な態度が必要とされ，「学びに向かう力，人間性等」と深く関わっている。
・　また，数学的な見方・考え方は，関数領域のみならず，数と式や，図形など他の領域においても広く働かせることができるものである。
このように，「数学的な見方・考え方」は，数学的に考える資質・能力の育成に関して，数学の様々な領域において広く働かせるものであることに留意する必要がある。

以上のように，数学的な見方・考え方を働かせた学習活動は，数学的に考える資質・能力を育成する多様な機会を与えるとともに，数学や他教科の学習，日常や社会において問題を論理的に解決していく場面などでも広く生かされるものである。
例えば，広く社会に目を向けると，自然現象のみならず，
・　成分の含有量により年代測定をする考古学，
・　糖分量により癌（がん）を発見する核医学，
・　為替レートで経済状況を予測する経済学など，
様々な分野で生かされている。

このように，「数学的な見方・考え方」は，身近な生活のみならず，社会における賢明な意思決定や判断を行っていく上で必要な資質・能力を身に付ける際に有効に働くものである。
素数が活用された暗号化技術がクレジットカードやインターネット通販など日常生活のみならずグローバル社会における情報セキュリティを確保するための基盤となっているなど，初等的な数学的な見方・考え方であってもグローバルな社会において重大な役割を果たしている。

したがって，数学の学習において数学的な見方・考え方を働かせる機会を意図的に設定することが重要であり，数学や他教科の学習を通して，数学的な見方・考え方も更に豊かなものになると考えられる。

小学校算数科「数学的な見方・考え方」

（２）学び方

【「数学的活動を通して」について】

① 数学的活動

数学的活動とは，
事象を数理的に捉え，数学の問題を見いだし，問題を自立的，協働的に解決する過程を遂行することである。
これは，「生徒が目的意識をもって主体的に取り組む数学に関わりのある様々な営み」であるとする従来の意味をより明確にしたものである。

今回の改訂では，数学的に考える資質・能力を育成する上で，数学的な見方・考え方を働かせた数学的活動を通して学習を展開することを重視することとした。

② 問題発見・解決の二つの過程

数学的活動における問題発見・解決の過程には，主として二つの過程を考えることができる。
・　一つは，日常生活や社会の事象を数理的に捉え，数学的に表現・処理し，問題を解決し，解決過程を振り返り得られた結果の意味を考察する過程であり，
・　もう一つは，数学の事象から問題を見いだし，数学的な推論などによって問題を解決し，解決の過程や結果を振り返って統合的・発展的に考察する過程である。
これら二つの過程は相互に関わり合って展開される。

数学の学習過程においては，これらの二つの過程を意識しつつ，生徒が目的意識をもって遂行できるようにすることが大切である。
また，各場面で言語活動を充実し，それぞれの過程や結果を振り返り，評価・改善することができるようにすることも大切である。

これらの過程については，答申で示された次のようなイメージ図で考えることができる。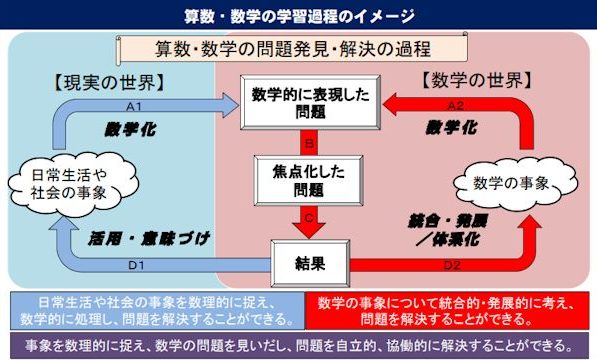
※　原本の図の出典は同じであるが白黒印刷である。出典:中央教育審議会「幼稚園，小学校，中学校，高等学校及び特別支援学校の学習指導要領等の改善及び必要な方策等について（答申）別添資料（2／3）『算数・数学科において育成を目指す資質・能力の整理』別添4-3 」平成28年12月21日[ONLINE]http://www.mext.go.jp/component/b_menu/shingi/toushin/__icsFiles/afieldfile/2017/01/10/1380902_3_2.pdf（参照2018/12/10）

【現実の世界】の部分を含む過程

イメージ図の左側の【現実の世界】の部分を含む過程は，日常生活や社会の事象を数理的に捉え，数学的に表現・処理し，問題を解決し，解決過程を振り返り得られた結果の意味を考察する過程である。

日常の事象や社会の事象を数理的に捉える過程を，このイメージ図では「日常生活や社会の事象の数学化」としている。
これは，現実世界の事象を考察する際に，目的に応じて必要な観点をもち，その観点から事象を理想化したり抽象化したりして，事象を数量や図形及びそれらの関係などに着目して数学の舞台にのせて考察しようとすることである。
数学的な見方・考え方を働かせ，事象を目的に応じて数学の舞台にのせたものが，イメージ図の「数学的に表現した問題」である。
そして，数学的に表現した問題をより特定なものに焦点化して表現・処理し，得られた結果を解釈したり，類似の事象にも活用したりして適用範囲を拡（ひろ）げる。

【数学の世界】に含まれる過程

数学の事象から問題を見いだし，数学的な推論などによって問題を解決し，解決の過程や結果を振り返って統合的・発展的に考察する過程は，イメージ図の右側の【数学の世界】に含まれる過程である。

数学の事象から問題を見いだす過程を，イメージ図では「数学の事象の数学化」としている。
これは，数学的な見方・考え方を働かせ，数量や図形及びそれらの関係などに着目し，観察や操作，実験などの活動を通して，一般的に成り立ちそうな事柄を予想することである。
この予想した事柄に関する問いが「数学的に表現した問題」となる。
そして，数学的に表現した問題をより特定なものに焦点化して表現・処理したり，得られた結果を振り返り統合的・発展的に考察したりする。

具体的には，幾つかの連続する整数の和に着目し，個別・具体的な場合を計算するなどして，そこにおいて成り立つ規則性に気付き，予想を立てる。
そして，例えば「三つの連続する整数の和はいつでも３の倍数になるのであろうか」という数学的に表現した問題において，文字の式を用いてこの予想が正しいことを説明する。
説明を終えた後でも，深い学びを目指して，問題解決の過程や結果を振り返り，新たに幾つかの整数の和に着目することで，「等間隔に並んだ整数の和」や「連続する奇数個の整数の和」，「連続する偶数個の整数の和」などについても，統合的・発展的に考察する。

このような過程を通して，粘り強く考え続けようとすることは，数学を創造的に学ぶ上で大切なことである。

問題発見・解決の過程の指導上の留意点

このイメージ図は数学の問題発見・解決の過程全体を示しており，「数学的活動を通して」とは，単位授業時間においてこれらの過程の全てを学習することを求めるものではないことに留意する。

実際の数学の学習過程では，このイメージ図の過程を意識しつつ，指導において必要な過程を遂行し，その結果，これらの過程全体を自立的，協働的に遂行できるようにすることが大切である。

なお，中学校数学科においては，数学的活動を通して主体的・対話的で深い学びを実現するために，その主要な側面として，

1. 「日常の事象や社会の事象から問題を見いだし解決する活動」，
2. 「数学の事象から問題を見いだし解決する活動」，
3. 「数学的な表現を用いて説明し伝え合う活動」

の三つを〔数学的活動〕として各学年の内容として示している。

これらのことについては，第２章の第２節，第３章で詳しく述べる。

※　小学校算数科では，平成10年小学校学習指導要領から始まる「算数的活動」を，名称とともに小・中・高で一貫した「数学的活動」とした。

小学校算数科「学び方」

（３）資質・能力

【「数学的に考える資質・能力を育成すること」について】
今回の改訂では，数学の学習において「何を学ぶか」のみならず「何ができるようになるか」という観点から整理された育成を目指す資質・能力を示すこととした。

「数学的に考える資質・能力」とは，数学科の目標で示された三つの柱で整理された算数・数学教育で育成を目指す力のことである。
これらの資質・能力は，数学的な見方・考え方を働かせた数学的活動を通して，三つの柱をバランスよく育成することが必要である。また，これらの資質・能力は，数学の学習の基盤となるだけではなく，教科等の枠を越えて全ての学習の基盤として育んでいくことが大切である。

以下④から⑥では，中学校数学で育成を目指す資質・能力の三つの柱について解説する。

※　「④から⑥」は，本稿では３（１）から（３）

小学校算数科「資質・能力」

３　三つの柱

（１）知識及び技能

これは，育成を目指す資質・能力の柱の中の「知識及び技能」に関わるものである。
知識及び技能には，
・　概念的な理解や数学を活用して問題解決する方法の理解，
・　数学的に表現・処理するための技能
などが含まれる。

①　知識

中学校数学科で扱う基礎的な概念や原理・法則は，生活や様々な学習の基盤となるものである。ここで，概念や原理・法則を理解することは，数学の知識の裏付けとなり，技能の支えとなる。すなわち，概念や原理・法則の理解は，事実的知識の暗記や機械的技能の訓練ではなく，深い学びを実現する上で欠かすことができないものである。

例えば，文字を用いた式の計算，方程式を解くことなどの技能を学ぶ際には，その手続きの基礎に概念や原理・法則があることや，概念や原理・法則をうまく使って数学的な処理の仕方が考え出されることを理解することが大切である。

基礎的な概念や原理・法則を理解するということは，数学の特質からみて，より進んだ知識や技能を生み出すこと，発展的に考えることを可能にするものである。
したがって，基礎的な概念や原理・法則を理解できるようにするためには，基礎的な概念や原理・法則に基づく知識及び技能を，
・　問題発見・解決の過程において的確かつ能率的に用いるとともに，
・　様々な日常や社会の事象の考察に生かしたり，
・　より広い数学的な対象について統合的・発展的に考察したり
できるよう配慮することが大切である。

数学的活動を通した概念や原理・法則の理解に裏付けられた発展性のある知識及び技能こそが，生きて働く知識や技能なのである。

②　技能

問題発見・解決の過程を遂行するためには，事象を数学化したり，数学的に解釈したり，数学的に表現・処理したりすることが必要である。
問題発見・解決の過程には，
・　主として日常生活や社会の事象に関わる過程と，
・　数学の事象に関わる過程
がある。

日常生活や社会の事象に関わる過程での技能

日常生活や社会の事象は，そのままで数学の舞台にのせることはできないことがある。
そのため，事象を数学化する際には，事象に潜む関係を解明したり活用したりするなどのねらいに即して，事象を理想化したり単純化したり，条件を数学的に表現したりすることが必要とされる。
また，得られた数学的な結果について実際の問題の答えとして受け入れるかどうかを判断するために，数学的な結果を具体的な事象に即して解釈することも必要である。

このような問題発見・解決の基礎をなす技能を身に付けることにより，事象を数学の舞台にのせ，社会生活や自然界における事物・現象等の広い範囲にわたる事象について考察することができるようになる。

数学の事象に関わる過程での技能

数学の事象から問題を見いだし考察する過程において，事象を数学化する際には，
・　数量や図形などに関する性質や関係を調べるねらいに即して，事象を一般化したり拡張したり，条件を数学的に表現したりすることが必要とされる。
・　また，数量や図形などに関する性質や関係を，数学の用語や記号によって表現したり，数学的な推論に必要な仮定や，それによって得られた結論を表現したり読み取ったりすることも必要である。

このような問題発見・解決の基礎をなす技能を身に付けることにより，原初となる具体的な数学の問題から，条件を変えたり，条件を弛（ゆる）めたりするなどして新たに設定した問題へと統合的・発展的に考察することができるようになる。

生きて働く数学的な知識に支えられた技能

また，問題発見・解決の過程において，数学を適切に活用するためには，生きて働く数学的な知識に支えられた技能を習得することが大切である。
事象を数学化したり，数学的に解釈したり，数学的に表現・処理したりする技能は，
数学的な概念や原理・法則と相互に支え合い，一体的なものとして学ばれるものである。

このように，数学的な技能は，数学をどのように活用するのか，その方法についての理解と一体化したものとみなされる。

例えば，一次方程式を活用して数学の問題を解決するとき，
・　「ある数量に着目し，その数量を二通りに表し，それらを等号で結ぶ」という方法を用いることで，問題場面を一次方程式に表すことができることを知ることが大切である。
・　また，表された方程式は具体的な数量の意味を考えずに「等式の性質」に基づいて形式的に処理することができること，
・　さらには，表された方程式が問題場面の全ての条件を表現してはいないので，得られた方程式の解が実際の問題場面に即して意味をもつかどうかを吟味しなければならないことを知ることも大切である。

このように，問題解決に数学を活用する技能は，いわば「方法知」とでも呼ばれる問題解決する方法に関する知識と深く関わっているのである。

※　方法知を身に付ける：例えば，金槌とは「釘などを打ち込むのに使い，槌（つち）の頭または全部を鉄で作ったもの」という知識（内容知）だけではなく，柄の先端に近い方を軽く握り脇をやや締め，肘を中心に手首・肩を使い槌の重みと振り落としの力を利用して釘を打ち込むという基本的な使い方（方法知）が分かって，この先，板の接合などの必要があれば，金槌を使って釘を打ち込むことができるあろうと予測できるようにすることである。（筆者）
※　内容知は，真偽で評価し得る知識であるのに対して，方法知は，ある種の事柄を行う能力がある，或いはその仕方を知っている，今後もその事柄を成し遂げる（或いは正しく把握する）ことができるだろうと予測できるようにすることである。
※　knowing−that(内容知)とknowing−how(方法知)に関する標準的見解：
a）knowing−howは，ある命題が真であるとかある事実が成立するということを知ることにあるのではない。knowimg−howは（いかなる形式の）knowing−thatにも還元できないし，同一視できない。
b）いかにGするかを知っている（knowing-how to G）ということは，Gできること，すなわちGする力量をもつことにある。knowing−howの帰属は，行為者に能力（abilities）ないし力量（capacities）を帰属することである 。
出典　池吉琢磨，中山康雄(2009)「knowing-thatとknowing−howの区別」[ONLINE]https://www.jstage.jst.go.jp/article/kisoron/37/1/37_KJ00007180013/_pdf(cf 2020.05.26)

小学校算数科「知識及び技能」

（２）思考力，判断力，表現力等

これは，育成を目指す資質・能力の柱の中の「思考力，判断力，表現力等」に関わるものである。
思考力，判断力，表現力等は，問題を見いだしたり，知識及び技能を活用して問題を解決したりする際に必要である。

数学を活用して事象を論理的に考察する力

数学を活用して事象を論理的に考察する力は，様々な事象を数理的に捉え，数学的に表現・処理し，問題を解決し，解決過程を振り返り得られた結果の意味を考察する過程を遂行することを通して養われていく。
・　数学が活用できるように事象を数学化するには，ねらいに即して事象から条件や仮定を設定し，数学の問題として表現することが必要である。
・　また，問題の解決に当たっては，解決の見通しをもつとともに，その解決の正しいことを確かな根拠から論理的に考察する力が必要である。
そのような力を養う際に，
・　一方では，直観的，帰納的，類推的に推論する力を養うとともに，
・　他方では演繹的に推論する力を養う
ことも重要である。
これらの二つの面を共に伸ばして，問題の発見と解決に役立てていくことが大切であり，特に，得られた結果の意味を，条件や仮定に即して考察する機会を設けることが重要である。

数量や図形などの性質を見いだし統合的・発展的に考察する力

数量や図形などの性質を見いだし統合的・発展的に考察する力は，主に，数学の事象から問題を見いだし，数学的な推論などによって問題を解決し，解決の過程や結果を振り返って統合的・発展的に考察する過程を遂行することを通して養われていく。

数学が歴史的に発展しているのは，一旦解決された問題やその解決過程を振り返り，問題の条件や仮定を見直したり，共通する性質を見いだしたり，概念を一般化したり拡張したりする活動を数学者たちが続けているからである。
したがって，数学の事象についての問題解決の指導に当たっては，振り返ることによる新たな問題の発見を生徒に促すことが大切である。その際，得られた解決に関して，
・　「他に分かることがないかを考えること」，
・　「問題解決の過程を振り返り，本質的な条件を見いだし，それ以外の条件を変えること」，
・　「問題の考察範囲自体を拡（ひろ）げること」，
・　「類似な事柄の間に共通する性質を見いだすこと」
などの新しい知識を得る視点を明確にしつつ，さらなる活動を促すことも大切である。

数学的な表現を用いて事象を簡潔・明瞭・的確に表現する力

数学では言葉や数，式，図，表，グラフなどの様々な表現を用いる。
数学的な表現は物事の特徴を抽象し簡潔・明瞭に表すとともに，考察対象を一般的に表す。このように数学的な表現は，それを使わないで考えるよりも質の高い思考を可能にする。

他方で，数学的な表現には，例えば，
・　式は数量やその関係について一般的な表現や形式的な操作を可能にし，
・　図は視覚的な把握を容易にし，
・　表は変化の規則性を示唆し，
・　グラフは事象の変化の様子を視覚的に把握することを容易にする
など，それぞれに長所がある。

指導に当たっては，目的に応じて的確な数学的な表現を選択したり，一つの対象の幾つかの数学的な表現を相互に関連付けたりすることを通して，事象の本質を捉えたり，理解を深めたりするように配慮することが大切である。
また，その際に，問題解決の過程を振り返りながら，表現を自立的，協働的に修正・改善したり，議論の前提を明確にしたりしながら，問題の特徴や本質を捉えることも大切である。

小学校算数科「思考力，判断力，表現力等」

（３）学びに向かう力，人間性等

これは，育成を目指す資質・能力の柱の中の「学びに向かう力，人間性等」に関わるものである。
学びに向かう力，人間性等には，数学のよさを実感して粘り強くかつ柔軟に考えようとすることなどが求められる。

例えば，IEAの国際数学・理科教育動向調査(TIMSS2015)における我が国の質問紙調査の結果では，数学を学ぶ楽しさや，実社会との関連に対して肯定的な回答をする割合も改善が見られる一方で，いまだ諸外国と比べると低い状況にあるなど学習意欲面で課題がある。
また，小学校と中学校の間で算数・数学の勉強に対する意識に差があり，小学校から中学校に移行すると，数学の学習に対し肯定的な回答をする生徒の割合が低下する傾向にある。

これらのことからも，生徒が，数学は楽しい，数学は面白いと実感し，数学が得意であるという自己肯定的な態度を養うことが大切である。

数学的活動の楽しさ

生徒が数学の学習に主体的に取り組むことができるようになるためには，数学的活動の楽しさや数学のよさを実感することが大切である。

「数学的活動の楽しさ」については「数学のよさ」とともに「実感」することとしている。
これは，学びを支える情意的な側面を大切にすること，すなわち，数学を学ぶことへの意欲を高めるとともに，数学的活動に主体的に取り組むことを大切にするとの趣旨によるものである。

単にでき上がった数学を知るだけでなく，事象を理想化したり抽象化したりして数学の舞台にのせ，事象に潜む法則を見つけたり，観察や操作，実験などによって数や図形の性質などを見いだし，見いだした性質を発展させたりする活動などを通して数学を学ぶことを重視することが大切である。
さらに，自立的，協働的な活動を通して数学を学ぶことを体験する機会を設け，その過程で様々な工夫，驚き，感動を味わい，数学を学ぶことの面白さ，考えることの楽しさを味わえるようにすることが大切である。

数学のよさ

数学的に考えることのよさ，数学的な表現や処理のよさ，数学の実用性などを実感し，様々な事象の考察や問題解決に数学を活用しようとする態度を育成するためには，何よりも「数学のよさ」を実感できるようにすることが大切である。

ここで，「数学のよさ」とは，例えば
・　「数量の関係を方程式で表すことができれば，形式的に変形して解を求めることができる」といった数学的な表現や処理のよさや，
・　数量や図形などに関する基礎的な概念や原理・法則のよさ，
・　数学的な見方・考え方を働かせることのよさ
などを意味する。また，
・　数学が生活に役立つことや数学が科学技術を支え相互に関わって発展してきていることなど，社会における数学の意義や価値
も含まれる。

数学のよさを実感できるようにするためには，
・　数学を学ぶ過程で，数学的な知識及び技能を確実に用いることができるようになったり，
・　思考力，判断力，表現力等を発揮することによって能率的に物事を処理できるようになったり，
・　事柄を簡潔かつ明瞭に表現して的確に捉えることができるようになったりする
成長の過程を振り返るなどして明確に意識できるようにすることが大切である。

数学を生活や学習に生かそうとする態度

数学的活動の楽しさや数学のよさは，数学が生活や他教科等の学習において生かされることなどを通して実感される。それゆえ，数学が日常生活や社会生活において，また他教科の学習やその後の人生において必要不可欠なものであることに気付かせることが大切である。

現代の社会生活において思慮深く賢明な市民として生きていくには，様々な事象の考察に際し，見方・考え方を自在に働かせられるようにすることが大切である。
・　数量の性質を文字を用いて一般的に考察したり，
・　図形の性質を直観的，論理的に考察したり，
・　数量の関係を変化や対応を捉えて考察したり，
・　不確定な事象の起こりやすさやデータの傾向を読み取って考察したり
する際など，数学的な見方・考え方を働かせた数学的活動を通して，生活や学習に果たす数学の役割に気付くことができるようにし，数学を積極的に活用しようとする態度を養うことが大切である。
そのような態度を養うことにより，知識基盤社会において学びに向かう力や人間性等を養うことにつながる。

問題解決の過程を振り返って評価・改善しようとする態度

数学的に問題解決する過程では，事象を数学的に表現し，構想や見通しを立て，試行錯誤により解決し，結果を導くなどする。しかし，結果が得られたところで終わるのではなく，結果の妥当性を検討することが大切である。その際，解決の方法や内容，順序を見直したり，自らの取り組みを客観的に評価したりすることが大切であり，これらが評価・改善しようとする態度であるといえる。

問題解決の過程を振り返って，評価・改善しようとする態度を育成するためには，協働的な活動を通して，生徒同士の多様な考えを認め合うことも重要である。多様な考えを相互に出し合い認め合うことは，よりよい問題解決を実現するだけでなく，次の機会に向けた新たな発想を引き出すことにつながる。

価値観の多様化する現代社会においては，特定の見方・考え方に固執するのではなく，柔軟に思考し，事象を多様な視点から捉え，それらを比較するなどして新しい考えを創造しようとする態度が重要となっている。

小学校算数科「学びに向かう力，人間性等」

出典:文部科学省「中学校学習指導要領解説数学編　第２章 数学科の目標及び内容　第１節 数学科の目標　１ 教科の目標」平成29年６月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387018_4_1.pdf（参照2018/03/30）を加工して作成
平成29年7月版[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2018/05/07/1387018_4_2.pdf (cf:2018-12-16) 平成29年7月版での訂正部分を本稿修正済








資料

算数・数学科において育成を目指す資質・能力の整理

中教審添付資料「算数・数学科において育成を目指す資質・能力の整理」において，「 知識・技能」「思考力・判断力・表現力等」「学びに向かう力・人間性等」という資質・能力の三つの柱と「資質・能力の育成のために重視すべき学習過程等の例」として，資質・能力と学習過程が学校段階ごとに示されています。

算数・数学科において育成を目指す資質・能力の整理

出典:中央教育審議会「幼稚園，小学校，中学校，高等学校及び特別支援学校の学習指導要領等の改善及び必要な方策等について（答申）別添資料（2／3）『算数・数学科において育成を目指す資質・能力の整理』別添4-1 」平成28年12月21日[ONLINE]http://www.mext.go.jp/component/b_menu/shingi/toushin/__icsFiles/afieldfile/2017/01/10/1380902_3_2.pdf（参照2018/04/03）