- 小学校算数科における「数学的な見方・考え方」のうち,「数学的な見方」とは何か,具体的にどのような見方をするのでしょうか。
- 「数学的な見方」とは,事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えることです。
- 例えば,大きな数を数えるとき,「数のまとまり」に着目すると,手際よい比べ方や数え方を考えることができます。
- また,二直線の位置関係に着目すると,それらの関係には,交わる場合と交わらない場合があることが分かります。
- 四角形を調べる場面で,平行といった直線の位置関係に焦点化したとき,平行が何組あるかに着目することで,図形を分類できます。
- 図形を構成する要素である辺の長さや角の大きさに着目することで,さらに図形の性質が見いだせます。
この「数のまとまり」や「図形を構成する要素及びそれらの位置関係」などは,どのような視点で物事を捉えるのかという,物事の特徴や本質を捉える視点を意味します。
1 数,量,形を捉える視点としての数学的な見方
小学校学習指導要領算数科の目標は,次のとおりです。
数学的な見方・考え方を働かせ,数学的活動を通して,数学的に考える資質・能力を次のとおり育成することを目指す。
(1) 数量や図形などについての基礎的・基本的な概念や性質などを理解するとともに,日常の事象を数理的に処理する技能を身に付けるようにする。
(2) 日常の事象を数理的に捉え見通しをもち筋道を立てて考察する力,基礎的・基本的な数量や図形の性質などを見いだし統合的・発展的に考察する力,数学的な表現を用いて事象を簡潔・明瞭・的確に表したり目的に応じて柔軟に表したりする力を養う。
(3) 数学的活動の楽しさや数学のよさに気付き,学習を振り返ってよりよく問題解決しようとする態度,算数で学んだことを生活や学習に活用しようとする態度を養う。
柱書のはじめには,「数学的な見方・考え方を働かせ,数学的活動を通して」とあります。
これは算数科学習指導の基本的な考え方を述べたものです。それを通して,(1)から(3)に示される「数学的に考える資質・能力」の育成を目指します。
数学的に考える資質・能力の育成に当たっては,算数科の特質に応じた見方・考え方が重要な役割を果たします。
本稿では,「数学的な見方とは何か,具体的にどのような見方をするのか」などについて考察します。
(1)「数のまとまり」に着目する
例えば,小学校第1学年「数と計算」領域に,次の指導内容があります。
| A 数と計算(1)イ 「数のまとまりに着目し,数の大きさの比べ方や数え方を考え,それらを日常生活に生かすこと。」 |
この指導内容では,「数のまとまり」に着目することが数学的な見方です。

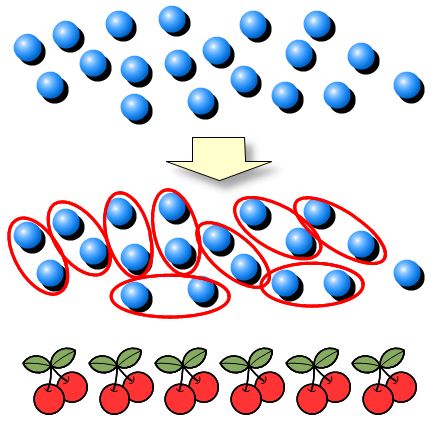
ある対象の個数を数えるとき,対象の数が大きくなると数えにくくなります。
そのとき,間違えないように数えることや,より手際よい数え方を工夫する必要が出てきます。
【問い】「どうすれば間違えないで手際よく数えられるだろう。」
これが子どもの問いです。
「1つ1つ数えるのは面倒だ。どうすれば手際よく数えられるか。」
「1つずつが面倒なら,2つずつならどうか。」
「数のまとまり」に目をつけると数えやすい。
このような意識の流れから,2ずつ数えるなど,数のまとまりに着目して数えたり比べたりする考えを児童が見いだせるようにします。
学習のまとめでは,
| 「2個ずつだと,数えやすかった。」 「5個ずつ数えると,はやく数えられた。」 |
など「数のまとまり」に着目するよさを確かめることが大切です。
このことが,もっと大きな数,100までの数のようなを数えるときに10のまとまりをつくることにつながり,十進位取り記数法の仕組みを理解する基礎となります。
このように「数の大きさの比べ方や数え方」を考えるとき,「数のまとまり」に着目すると,手際よい比べ方や数え方を考えることができます。
(2)「図形を構成する要素及びそれらの位置関係」に着目する
小学校第4学年「図形」領域に,次の指導内容があります。
| B 図形 (1)イ 「図形を構成する要素及びそれらの位置関係に着目し,構成の仕方を考察し図形の性質を見いだす…後略…」 |
図形を構成する要素及びそれらの位置関係に着目し,構成の仕方を考察し図形の性質を見いだす指導内容です。
この指導内容では,「図形を構成する要素及びそれらの位置関係」に着目することが数学的な見方です。
正方形,長方形,平行四辺形,ひし形,台形は,辺や角などで構成されます。
児童はこれまで角を一つの図形と認識しています。四角形を構成する角を,辺と辺でつくられる図形と見ると,角の捉え方が変わってきます。
図形の構成要素である辺に着目して辺の見方を広げると,辺は直線と見ることができます。
辺を直線と見るにはやや難しさがあるので,ここでは直線を推測しやすい教材の工夫が期待されます。
さて,図形の辺を直線と捉えると,二直線の交わり方はいろいろです。ここで 二直線の位置関係が問題となります。
そして,二直線の位置関係に着目すると,それらの関係には,交わる場合と交わらない場合があることが分かります。
さらに,交わる場合においては,特殊な場合として 90度で交わる場合のあることが分かってきます。
二直線の位置関係に着目することで,道路の交わりから二直線の交わり,そして二直線の位置関係へと認識が深まってきたのです。
このような考察により,
| 二直線の関係には,特殊な場合として,垂直に交わる場合と,交わることのない平行の場合がある |
ことが引き出されます。
そして,平行といった直線の位置関係に焦点化したとき,平行が何組あるかに着目することで,図形を分類できます。
| 四角形を取り上げると,平行が一 組しかない四角形の台形と二組ある四角形の平行四辺形とひし形に分類できます。 |
さらに,図形を構成する要素である辺の長さや角の大きさに着目することで,さらなる図形の性質が見いだされます。
| 辺の長さに着目すると,平行な二組の辺の長さはそれぞれ等しいこと(平行四辺形の性質) その特殊な場合として,二組の平行な辺の長さが全て等しい場合(ひし形)のあること |
さらに,角の大きさや,対角線の長さや位置関係を考えることで,さらなる性質が引き出されます。
そして,見いだされた性質を基にすると,図形を作図することが可能になると共に,身の回りから,平行四辺形,ひし形,台形の形をした具体物を見付けることができます。
角の大きさや,対角線の長さや位置関係に着目することで,それらの図形の認識が深まってきたのです。
この「数のまとまり」や「図形を構成する要素及びそれらの位置関係」は,どのような視点で物事を捉えるのかという,物事の特徴や本質を捉える視点を意味します。
これらの視点に着目する数学的な見方で対象を捉え,数学的な考え方で思考を進めていくことによって,問題を解決したり新たな見方・考え方を発見したりすることができるようになります。
2 数学的な見方・考え方を働かせる
(1)「数学的な見方・考え方」を働かせる
学習指導要領の「指導計画の作成と内容の取扱い」では,数学的な見方・考え方を働かせることについて,次のように配慮するよう求めています。
学習指導要領第3節算数「第3 指導計画の作成と内容の取扱い」
1 指導計画の作成に当たっては,次の事項に配慮するものとする。
(1) 単元など内容や時間のまとまりを見通して,その中で育む資質・能力の育成に向けて,数学的活動を通して,児童の主体的・対話的で深い学びの実現を図るようにすること。
その際,数学的な見方・考え方を働かせながら,日常の事象を数理的に捉え,算数の問題を見いだし,問題を自立的,協働的に解決し,学習の過程を振り返り,概念を形成するなどの学習の充実を図ること。
このように,算数の学習において,「数学的な見方・考え方」を働かせながら,知識及び技能を習得したり,習得した知識及び技能を活用して課題を探究したりすることで,生きて働く知識の習得が図られ,技能の習熟にもつながるとともに,日常の事象の課題を解決するための思考力,判断力,表現力等が育成されます。
そして,数学的に考える資質・能力が育成されることで,「数学的な見方・考え方」も更に成長していくと考えられます。
今回の学習指導要領の改訂で,小学校算数科で育成する資質・能力の三つの柱を明確化したことにより,「数学的な見方・考え方」は,どのような視点で物事を捉え,どのような考え方で思考をしていくのかという,物事の特徴や本質を捉える視点や,思考の進め方や方向性を意味することとなりました。
(2)数学的な見方・考え方とは
数学的な見方
事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
数学的な考え方
目的に応じて図,数,式,表,グラフ等を活用し,根拠を基に筋道を立てて考え,問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら統合的・発展的に考えること
これらから,算数科における「数学的な見方・考え方」とは,以下のように整理できます。
数学的な見方・考え方
「事象を数量や図形及びそれらの関係などに着目して捉え,根拠を基に筋道を立てて考え,統合的・発展的に考えること」
「数学的な見方・考え方」は,数学的に考える資質・能力を支え,方向付けるものであり,算数の学習が創造的に行われるために欠かせないものです。
また,児童一人一人が目的意識をもって問題解決に取り組む際に積極的に働かせていくものです。
その意味で「数学的な見方・考え方」は,数学的に考える資質・能力の三つの柱の全てに対して働かせるものです。
そして,算数の学習を通じて,「数学的な見方・考え方」が更に豊かで確かなものとなっていきます。
また,「数学的な見方・考え方」は,算数の学習の中で働かせるだけではなく,大人になって生活していく上でも重要な働きをします。
算数の学びの中で鍛えられた見方・考え方を働かせながら,世の中の様々な物事を理解し思考し,よりよい社会や自らの人生を創り出していくことが期待されます。
文部科学省「小学校学習指導要領解説算数編 第2章 算数科の目標及び内容 第1節 算数科の目標 1教科の目標」平成29年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_1_1.pdf(参照2018/03/12)
3 数学的な見方の具体の視点
数学的な見方の具体の視点には,「数のまとまり」や「図形を構成する要素及びそれらの位置関係」の他に,以下のものがあります。
学習指導要領の「2内容 」に「イ 次のような思考力,判断力,表現力等を身に付けること。 」として「思考力,判断力,表現力等」の指導内容が示されています。そこで直接文字化される数学的な見方の視点は,以下のとおりです。
直接文字化される数学的な見方の視点
| A 数と計算 | B 図 形 | |
|---|---|---|
| 視点 | 数の表し方の仕組み 数のまとまり 数を構成する単位 分数の表現 分数の意味や表現 数の意味と表現,計算について成り立つ性質 乗法及び除法 乗法及び除法の意味 数量の関係 問題場面の数量の関係 日常の事象における場面 そろばんの仕組み 二つの数量の対応や変わり方 |
ものの形 図形を構成する要素 図形の角の大きさ 図形を構成する要素の位置関係 平面や空間における位置を決める要素 面積の単位や図形を構成する要素 体積の単位や図形を構成する要素 図形間の関係 図形の性質 |
| C 測 定 | C 変化と関係 | |
| 視点 | 身の回りのものの特徴 時間の単位 |
伴って変わる二つの数量とそれらの関係 異種の二つの量の割合として捉えられる数量の関係 日常の事象における数量の関係 |
| D データの活用 | ||
| 視点 | データの個数 データを整理する観点 目的に応じてデータを集めて分類整理し,データの特徴や傾向 概括的に捉えること 事象の特徴 |
文部科学省「小学校学習指導要領 第2章各教科 第3節算数 第2各学年の目標及び内容」平成29年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2018/03/29/1384661_4_2.pdf(参照2018/04/14)
上記の視点に着目する数学的な見方は,数学的な考え方など思考力,判断力,表現力等とともに指導内容を伴うことで明確になります。
このことから,次に,五つの領域で身に付ける思考力,判断力,表現力等を数学的な見方・考え方と対応する形で示します。
なお,下の表は左右にスクロールできます。
「各学年の目標(2)」解説:5領域で身に付ける思考力,判断力,表現力等と数学的な見方・考え方
| A 数と計算 | B 図 形 | C 測 定 | C 変化と関係 | D データの活用 | |
|---|---|---|---|---|---|
| 第1学年 | ものの数に着目し,具体物や図などを用いて数の数え方や計算の仕方を考える力を養う。
数のまとまりや数量の関係に着目して,ブロックや数え棒といった具体物や図などを使って数の数え方や計算の仕方を考えたり,その過程を表現したりすることを重視するとともにそれらを日常生活に生かすことを重視する。 |
ものの形に着目して特徴を捉えたり,具体的な操作を通して形の構成について考えたりする力を養う。
身の回りにある様々なものの形に着目してその特徴に関心をもつとともに,空き箱や色板,折り紙などの具体物を使って形を組み合わせたり分解したり,動かして形を変形させてみたりなどの操作を通して形の構成について考えることを重視する。 |
身の回りにあるものの特徴を量に着目して捉え,量の大きさを比べる方法を考える力を養う。
長さ,広さ,かさなどの量から身の回りの事象の特徴を捉え,実験実測を通して量の大きさの比べ方を見いだす。 |
データの個数に着目して身の回りの事象の特徴を捉える力を養う。
身の回りにあるデータに関心をもって,事象の特徴をデータの個数に着目して大小や順番を捉えることができるようにする。 |
|
| 第2学年 | 数とその表現や数量の関係に着目し,必要に応じて具体物や図などを用いて数の表し方や計算の仕方などを考察する力を養う。
具体物などを用いることを通して,身の回りの数への関心を高め,数についての感覚を豊かにするとともに数の大きさや仕組みに着目して表し方を考える。 |
平面図形の特徴を図形を構成する要素に着目して捉えたり,身の回りの事象を図形の性質から考察したりする力を養う。
この学年から身の回りの事象を図形として捉え,図形の特徴を図形を構成する要素に着目して捉えたり図形の性質から考察したりすることを重視する。 |
身の回りにあるものの特徴を量に着目して捉え,量の単位を用いて的確に表現する力を養う。
長さ,かさの量から身の回りの事象の特徴に着目し,実験・実測を通して目的に応じた普遍単位を用いることで量を的確に表現したり比べたりすることを重視する。 |
「身の回りの事象をデータの特徴に着目して捉え,簡潔に表現したり考察したりする力」を養う。
身の回りの事象をデータを整理する観点に着目し,その事象の特徴を簡単な表やグラフに表して考察することができるようにする。 |
|
| 第3学年 | 数とその表現や数量の関係に着目し,必要に応じて具体物や図などを用いて数の表し方や計算の仕方などを考察する力を養う。
身の回りの数や数量の関係への関心を高め,数についての感覚を一層豊かにするとともに数の大きさや構造に着目して表し方を考え,日常生活に生かせるようにする。 |
平面図形の特徴を図形を構成する要素に着目して捉えたり,身の回りの事象を図形の性質から考察したりする力を養う。
身の回りの事象を図形として捉え,図形の特徴を図形を構成する要素に着目して捉えたり図形の性質から考察したりすることを重視する。 |
身の回りにあるものの特徴を量に着目して捉え,量の単位を用いて的確に表現する力を養う。
長さ,重さの量から身の回りの事象の特徴に着目し,実験・実測などを通して目的に応じた普遍単位を用いることで量を的確に表現したり単位を統合的に捉えたりすることを重視する。 |
身の回りの事象をデータの特徴に着目して捉え,簡潔に表現したり適切に判断したりする力を養う。
身の回りの事象のデータを整理する観点に着目し,その事象の特徴を簡単な表や棒グラフに表すとともにそれを基に適切な判断ができるようにする。 |
|
| 第4学年 | 数とその表現や数量の関係に着目し,目的に合った表現方法を用いて計算の仕方などを考察する力を養う。
数やその表現の仕方及び数量の関係に着目するとともに数の表現方法を統合的に捉えたり目的に合わせて考察したり,それらを日常生活に生かせるようにしたりする。 |
図形を構成する要素及びそれらの位置関係に着目し,図形の性質や図形の計量について考察する力を養う。
平面図形及び立体図形を平行・垂直などの図形を構成する要素に着目しながら,図形の性質や位置の表現方法を見いだしたり,それを基に既習の基本図形を捉えなおしたり日常の事象の考察に生かしたりすることを重視する。 |
変化や対応の特徴を見いだして,二つの数量の関係を表や式を用いて考察する力を養う。
低学年での数量の関係の学習を踏まえて,日常の事象における数量の関係に着目し,図や表,式などを用いて,変化や対応の関係やある二つの数量の関係と別の二つの数量の関係との比べ方を考察するとともに,その結果を日常生活で生かせるようにする。 |
目的に応じてデータを収集し,表やグラフに的確に表現し,それらを用いて問題解決したり,解決の過程や結果を多面的に捉え考察したりする力を養う。
第3学年までの学習に加えて,身の回りの事象から目的に応じたデータの収集,表や折れ線グラフを用いた問題解決及び解決過程や結果の多面的な考察を重視することが加わった。 |
|
| 第5学年 | 数とその表現や数量の関係に着目し,目的に合った表現方法を用いて数の性質や計算の仕方などを考察する力を養う。
数やその表現の仕方及び数量の関係に着目するとともに数の表現方法を統合的に捉えたり目的に合わせて考察したり,それらを日常生活に生かせるようにしたりする。 |
図形の性質や図形の計量について考察する力を養う。
平面図形を合同の視点から,図形を構成する要素や図形間の関係に着目しながら,図形の構成の仕方やその性質を見いだし論理的に説明したり,それを基に既習の基本図形を捉え直したり日常の事象の考察に生かしたりすることを重視する。 |
伴って変わる二つの数量やそれらの関係に着目し変化や対応の特徴を見いだして二つの数量の関係を表や式を用いて考察する力を養う。
これまでの数量の関係の学習を踏まえて,日常の事象における伴って変わる二量及びそれらの関係に着目し,図や表,式などを用いて,簡単な比例における変化や対応の考察や割合や単位量当たりの大きさにおける目的に応じた大小の比較及び表現をするとともに,それらを日常生活で生かせるようにする。 |
目的に応じてデータを収集し,表やグラフに的確に表現し,それらを用いて問題解決したり,解決の過程や結果を多面的に捉え考察したりする力を養う。
第4学年の学習に引き続いて,身の回りの事象から目的に応じたデータの収集,表や帯グラフや円グラフなどへの適切な表現,それを用いた問題解決及び解決過程や結果の多面的な考察を重視する。 |
|
| 第6学年 | 数とその表現や計算の意味に着目し,発展的に考察して問題を見いだすとともに,目的に応じて多様な表現方法を用いながら数の表し方や計算の仕方などを考察する力を養う。
数やその表現の仕方及び数量の関係に着目するとともに数の表現方法を目的に合わせて考察したり,それらを日常生活に生かせるようにしたりする。 |
図形を構成する要素や図形間の関係などに着目し図形の性質や図形の計量について考察する力を養う。
平面図形を対称の視点から,図形を構成する要素や図形間の関係に着目しながら,図形の構成の仕方やその性質を見いだし説明したり,それを基に既習の基本図形を捉えなおしたり日常の事象の考察に生かしたりすることを重視する。 |
変化や対応の特徴を見いだして,二つの数量の関係を表や式,グラフを用いて考察する力を養う。
これまでの数量の関係の学習を踏まえて,日常の事象における伴って変わる二つの数量及びそれらの関係に着目し,図,表,グラフ,式などを用いて,比例や反比例における変化及び対応や比における数量の関係の比べ方を考察するとともに,その結果を日常生活で生かせるようにする。 |
身の回りの事象から設定した問題について,目的に応じてデータを収集し,データの特徴や傾向に着目して適切な手法を選択して分析を行い,それらを用いて問題解決したり,解決の過程や結果を批判的に考察したりする力を養う。
これまでの学習で学んだ統計の問題解決過程を生かして,身の回りの事象から目的に応じたデータの収集,表や柱状グラフなどの選択と表現,それを用いた問題解決及び解決過程や結果の批判的な考察を重視する。 |
文部科学省「小学校学習指導要領解説 算数編 第3章各学年の目標及び内容」平成29年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_2.pdf(参照2018/04/15)
