算数科領域の標題は「数と計算」と「図形」で表現形式が異なる

算数科における領域の標題は，「Ａ数と計算」「Ｂ量と測定」と「Ｃ図形」で，表現の形式が異なるのはなぜでしょうか。

算数科の領域の標題には，「○と○」タイプの「Ａ数と計算」「Ｂ量と測定」とそうでない「Ｃ図形」「Ｄ数量関係」があります。
その理由は，A，B，Cの領域の名称については，なるべく対象とする概念とそれに対する操作とをまとめて領域の標題としているからです。
概念と操作を密接に結びつけて指導することが大切なことから，「（概念）と（操作）」の表現の形をとっています。
「図形」が対象となる概念だけを標題としているのは，図形に対する小学校での操作は多種多様であり，一つの用語で表現するのは当を得ないためです。
なお，「Ｄ数量関係」は，指導内容が他の領域とはやや異なる性格をもつことから名称の付け方は異なります。








領域の標題の表現形式

領域の標題の付け方

平成20年告示小学校学習指導要領の算数科の領域には，「Ａ数と計算」，「Ｂ量と測定」，「Ｃ図形」，「Ｄ数量関係」があります。
算数科で指導する内容はこれら４つの領域に分けて示されます。指導内容は，一つ一つ個別に列挙するより，共通な性格をもった内容を集めてグループ化して示す方が，とらえやすくなります。また，指導内容の系統も分かりやすくなります。
領域の構成は，
・　算数科の対象として大きな部分を占める数，量，図形の領域A，B，C
・　それらの対象を考察するときの共通な考え方や手法などを多く含む領域D
からなります。
これら４つの標題は名称の付け方に違いがあります。
「○と○」タイプの「Ａ数と計算」「Ｂ量と測定」とそうでないものです。

標題の付け方

A，B，Cの領域の名称は，なるべく
対象とする概念　と　それに対する操作
とをまとめて領域の標題とするようにしています。

例えば「Ａ数と計算」では，
「数」は対象とする概念であり，「計算」は数に対する操作です。
「数」は整数や小数，分数，「計算」は加法，減法，乗法，除法についての指導内容です。
「Ｂ量と測定」では，
「量」は対象とする概念であり，「測定」は量に対する操作です。
「量」は長さ，重さ，時間など，「測定」は長さや重さの単位や測定，時間の計算などについての指導内容です。

平成20年小学校学習指導要領では，面積や体積の単位と求め方は，「量と測定」領域の内容として整理されています。平成29年小学校学習指導要領では，「図形」領域の内容として取り扱われます。

	対象とする概念	概念に対する操作
数と計算	数	計算
量と測定	量	測定
図　形	図形	？

標題の付け方の基本的な考え方

例えば，「数と計算」では，
数の概念と数の操作である計算とは，密接に結びつけて指導することが大切であるという考え方に基づいて「（対象とする概念）と（それに対する操作）」という名称を用いています。
日常の事象を数で捉えるのは計算して何らかの結果を得ようとするときです。多くの場面では数と計算はセットで用いられます。
指導に際しては，数の概念の理解に基づいて計算の指導を行うことになりますが，計算を通して数の見方が豊かになり理解が深まります。
また，計算は数の理解なくして意味をもちません。
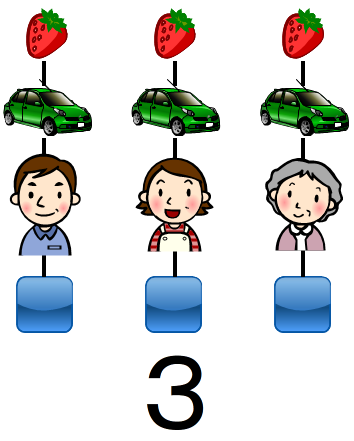イチゴが３個，自動車が３台，人が３人は，すべてブロック３個と同じです。それらは，数の３が共通します。数の３を「３」という記号で表します。他にも数の３は，ノート３さつのときもあります。
このような数の３という数の概念を理解できるようにすることが「数と計算」領域の「数」の指導内容です。

また，「計算」については，加法が用いられる場合とその計算の仕方を理解することなどがあります。
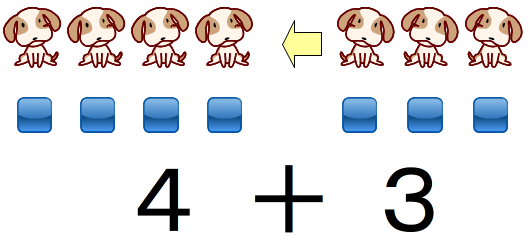
犬が４ひきいます。そこに，３びき来ました。合わせて何ひきになったでしょう。
ある数量に他の数量を追加したり，ある数量が増加したりしたときの数量の大きさを求める場合（増加）は加法を用います。そのことを４＋３と表します。加法は二つの集合を合わせた集合の要素の個数を求める演算です。したがって，４と３を合わせた数は7。答えは7ひきになります。これが「計算」の指導内容です。

「量と測定」も同様です。
量とはものの属性，状態を抽象したものです。
比較可能性や同値律を満たし，大小関係は推移律を満たすという性格をもちます。
この量は測定することが前提で取り扱われます。
単位を決め数値化することで客観的に大きさを示すことができます。測定結果を用いて比較したり変化を調べたりします。
指導に際しては，測定の学習のプロセスとして，直接比較，間接比較，任意単位による測定，普遍単位による測定の学習の過程を経ることで，量に対する理解が深まっていきます。

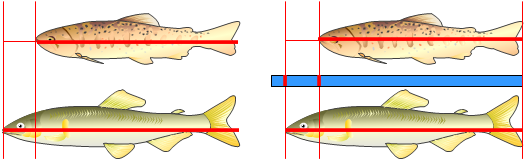
「どちらの魚の方が長いでしょう。」二つの長さを直接比べます。その際，一方の端の尾を揃えて，他方の端の口の位置によって長短を判断をします。間接比較では，ＡとＢの大きさをそれと等しい別のものに置き換えて，間接的に比較します。このような比較を通して，具体的なものの属性のうち，比べようとしている長さという量を抽象できるようにします。

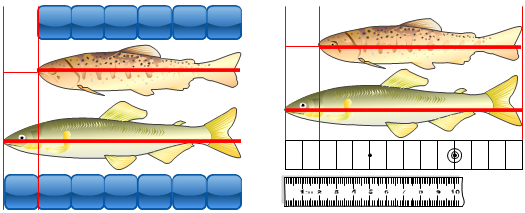
任意単位による測定では，ＡとＢの大きさを，それと同種の量の幾つ分という数値に置き換えて比較します。さらには，cmなどの普遍単位を使って長さを数値化します。すなわち普遍単位による測定です。
量の測定とは，量Ｂを基準にとるとき，他の量Ａがその何倍に等しいかを調べ，この何倍に当たる数ｐによって量Ａの大きさを表現することです。

このように，「Ａ数と計算」や「Ｂ量と測定」は，対象とする概念とそれに対する操作とを密接に結びつけて指導することが大切であるという考え方に基づいています。このことから，「量と測定」についても「（対象とする概念）と（それに対する操作）」という名称を用いています。








「Ｃ図形」の標題の意味

図形の操作は多種多様

「図形」については，単に対象となる概念だけを標題としています。
「図形」が対象となる概念だけを標題としているのは，図形に対する小学校での操作は多種多様であり，一つの用語で表現するのは当を得ないためです。※　文部省小学校指導書算数編第２章算数科の目標及び内容第２節算数科の内容１内容構成の考え方p.24

しかし，図形の概念は，それに対する操作と十分関連させて指導することが極めて重要です。
例えば，第１学年では，仲間分けしたり，形遊びをしたり，箱を積んだり，箱でものを作ったり，面を写し取ったりすることを通して，ものの形を認め，形の特徴について捉え，図形についての理解の基礎となる経験を豊かにします。色板の面を合わせたり，棒で線をつないだり，ジオボードの点を結んだりして図形をつくります。また，図形をいくつかの部分に分けたりもします。このような活動を様々に繰り返すことで，図形の捉えが豊かになり，図形に対する多様な見方が働くようになります。
このような図形に対する操作を通して図形の概念の理解が深まり，思考力等も育っていきます。

なお，図形の構成とは以下のようです。
「図形における具体的な操作などの活動としては，図形を移動させたり，切り離したり，定規やコンパスで線をひいたり，変形したりするなど多様なものがある。‥‥図形の構成とは，以上のような図形についての操作や，他の材料や用具を使うなどして新たな図形を作っていくことととらえることができる。」※　文部省小学校指導書算数編第２章算数科の目標及び内容第２節算数科の内容２各領域の内容の概観(平成元年６月)
「各学年における図形の内容では，観察や構成などの活動について示されている。観察や構成などの活動を通して，図形の意味を理解したり，図形の性質を見付けたり，図形の性質を確かめたりすることができるようになる。‥‥図形を実際に構成する具体的な活動には，紙を折ったり，切ったり，図形を移動させたり，切り離したり，変形したり，定規やコンパスを用いて作図したりするなどの活動がある。これらの活動は，図形学習における作業的・体験的な活動の例である。」小学校学習指導要領解説算数編第２章算数科の目標及び内容第２節算数科の内容２各領域の内容の概観(平成20年６月)
「図形の構成とは，身の回りの物や色板などを使って図形を作ったり，図形を分解したりすること，紙を折ったり切ったりして図形を作ること，コンパス，定規，分度器などを使って作図すること等を意味する。」小学校学習指導要領（平成29年告示）解説算数編第２章算数科の目標及び内容第２節算数科の内容２各領域の内容の概観(平成29年7月)

「数量関係」は異なる性格

「Ｄ数量関係」については，A，B，Cの領域の名称の付け方とは異なります。
「Ｄ数量関係」の指導内容が他の領域とはやや異なる性格をもつからです。
その領域の内容は，関数の考え，式を表現と読み，資料の整理と読みで構成されます。また，それらにおいて，数量やその関係を数，式，図，表，グラフなどに表したり調べたり，言葉を用いて表したり調べたり，判断したり，説明したりすることができるようにする指導内容です。先の加法の場面を式４＋３に表すことは式による表現であり，数量関係の指導内容です。

なお，「数量関係」において，第１学年から第６学年まで位置付けられていた式の表現と読みに関する内容を，平成29年改訂指導要領では，「数と計算」の考察に必要な式として捉え直し，「Ａ数と計算」領域に位置付け直すことになりました。

次の図の場面は，時間が１分，２分，‥‥と経つにつれて水の深さが2cm，4cm，‥‥と増えていく比例の場面です。時間に伴って変化する水の量など伴って変わる二つの数量の関係について考察することも数量関係の指導内容です。

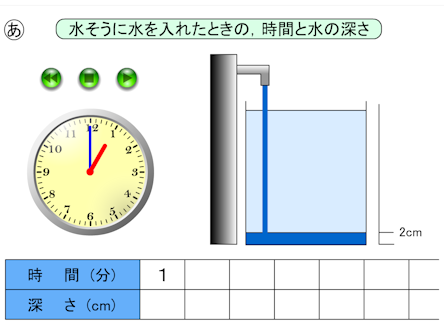
平成29年改訂指導要領では，「関数の考え」は「変化と関係」の指導内容となりました。そして「変化と関係」領域は上学年に位置付けられました。その理由は，従来の「数量関係」の領域における「関数の考え」が育成される内容が，伴って変わる二つの数量の関係（第４学年），簡単な比例（第５学年），比例と反比例（第６学年）など，上学年に位置付けられていたことを踏まえたからです。しかしながら，下学年においても，数や図形の等の考察において，数の関係を考察したり，変化の規則に注目したりする場面が多いことに注意が必要であり，そのような場面は「関数の考え」の素地指導をする重要な機会です。

平成29年改訂小学校学習指導要領算数科の領域

平成29年改訂小学校学習指導要領における算数科の領域は，
「Ａ数と計算」，「Ｂ図形」，「Ｃ測定」，「Ｃ変化と関係」，「Ｄデータの活用」
の５領域で構成されます。
算数科においては，これまでの約60年間については，
「数と計算」，「量と測定」，「図形」，「数量関係」
の４領域で構成されてきました。
領域の順序が数量関係と図形で前後したり，数量関係の設定学年が変更されたりすることはありましたが，算数科の領域は基本的に同じでした。平成29年改訂において領域の数や標題がこれまでと異なるのは，大きな変化といえます。

領域の標題については，「数と計算」は変更なし。「量と測定」は，「測定」とし新規に「Ｃ測定（下学年）」領域が設定されました。「これは，ものの属性に着目し，単位を設定して量を数値化して捉える過程を重視し，それぞれの量について，そこでの測定のプロセスに焦点を当てて学ぶことにしているから」です。これは，領域の標題を「（対象とする概念）と（それに対する操作）」しなかった理由と考えられます。
また，平成20年改訂小学校学習指導要領の算数科で指導する量は，長さ，面積，体積，時間，重さ，角の大きさ，速さなどです。平成29年の改訂では，面積，体積及び角の大きさは，図形の計量として「Ｂ図形」に，また，速さは，異種の二つの量の割合，単位量当たりの大きさとして「Ｃ変化と関係」に位置付けられました。このことにより，従来の「量と測定」領域での「量」の指導内容が相対的に減少しました。このことも領域名が「測定」となった理由の一つと推測されます。
平成29年改訂学習指導要領の領域構成等の詳細については，「４領域構成の中学校数学科とつながる５領域構成の算数科」または「数学的な見方・考え方と算数科領域のねらい」を参照ください。

平成20年改訂小学校学習指導要領第２章各教科第３節算数

領域	A	B	C	D
第１学年	数と計算	量と測定	図形	数量関係
第２学年	数と計算	量と測定	図形	数量関係
第３学年	数と計算	量と測定	図形	数量関係
第４学年	数と計算	量と測定	図形	数量関係
第５学年	数と計算	量と測定	図形	数量関係
第６学年	数と計算	量と測定	図形	数量関係

平成29年改訂小学校学習指導要領第２章各教科第３節算数

領域	A	B	C	D
第１学年	数と計算	図形	測定	データの活用
第２学年	数と計算	図形	測定	データの活用
第３学年	数と計算	図形	測定	データの活用
第４学年	数と計算	図形	変化と関係	データの活用
第５学年	数と計算	図形	変化と関係	データの活用
第６学年	数と計算	図形	変化と関係	データの活用

平成29年改訂学習指導要領における算数科の領域は，「知識及び技能」，「思考力，判断力，表現力等」をより明確にし，それらを育成する学習過程を計画できるようにすることや内容の系統性や発展性の全体を中学校数学科との接続を視野に入れ整理する観点から構成されました。
特に，以下の事項を中心として，内容領域を再編成しています。
・　「Ａ数と計算」の充実：「式の表現や読み」のＡ領域への位置付け
・　量を測定するプロセスの充実（下学年）と図形の計量的考察の充実（上学年）
・　変化や関係を把握する力の育成の重点化と統計教育の充実：数量関係領域の充実
また，児童の発達の段階を踏まえ，幼小の連携の視点，算数科と数学科の接続の視点から，第１学年，第２・３学年，第４・５学年，第６学年の四つの段階で育成を目指す資質・能力と，働かせる数学的な見方・考え方を明らかにしています。

参考　文部省「小学校指導書算数編」内容構成の考え方　平成元年6月