正方形に内接する正三角形を紙を折って作る

正方形の折り紙を使って，正方形に内接する正三角形を作るには，どのようにするとよいのでしょう。: 正方形の紙を折って，正三角形を作ることができます。
作り方
正方形各辺の垂直二等分線を折る。
正方形の特定の頂点を中心，その両隣の辺を半径として，垂直二等分線上に交点をとるようそれぞれ折り目を入れる。
それらの二つの折り目が，内接する正三角形の二辺。またその端点が，正三角形の三つの頂点となる。
証明
正方形各辺の垂直二等分線の性質，正方形の一辺を底辺とする正三角形の性質，折り返した三角形と元の三角形の計４つの合同な三角形の性質を使って説明できる。

１　作り方

（１）正方形の準備

まず，折り紙をなど正方形の紙を用意します。
長方形の場合は，短辺の一つの頂点を中心に，長辺に長さを移して，折り目を付けます。余った部分を取り除いて，開くと正方形ができます。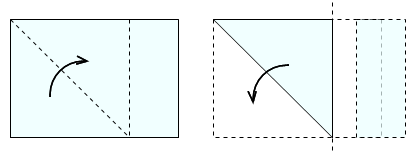折り方-0

（２）縦横に垂直二等分線を入れる

折り紙を，縦横に垂直に２等分します。
□ABCDのADをBCに重なるよう折り，折り目を付けて開きます。
同様に，ABをDCに重なるように折り，折り目を付けて開きます。
これらの折り目は各辺の垂直二等分線です。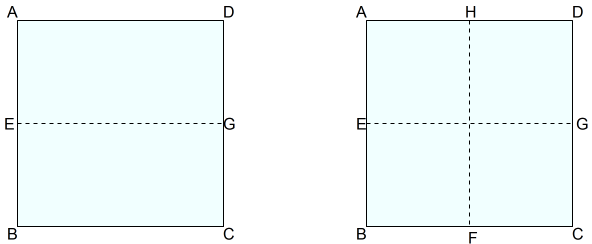折り方1

（３）正三角形の二つの辺を作る

左図のように，Aを中心として半径ABの円を描くようにABの長さを移し，HFとの交点B’をとります。その位置で折り目を入れます。
右図でも同様に，Aを中心として半径ADの円を描くようにADの長さを移し，EGとの交点D’をとります。その位置で折り目を入れます。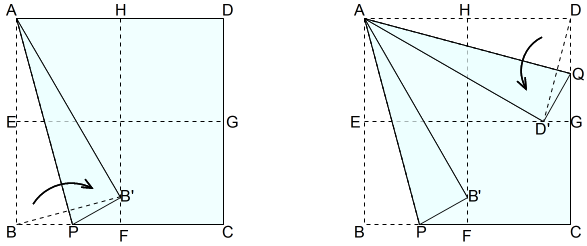折り方2

（４）三つ目の一辺を作る

PQを軸として，頂点Cを内側に折り返します。
そのとき，点B’と点D’の小さい三角形の部分も折れ曲がりますが，その部分に注意を払わなくて良いです。
注意すべきは，対称の軸PQが正確に一直線となるよう折り返すことです。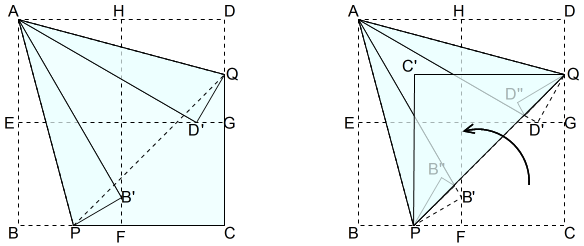折り方3
三角形APQが正三角形です。
この正三角形は，正方形に内接する正三角形の中で，最大面積の正三角形です。

２　正三角形の証明

（１）折り返した三角形は合同

折り返した部分について，折り返した三角形と元の三角形は合同です。
したがって頂点Aを頂点にもつ４つの合同な三角形があることになります。
なお，\(□ABCD\) の一辺の長さは，\(AB=BC=CD=DA=1\) とします。
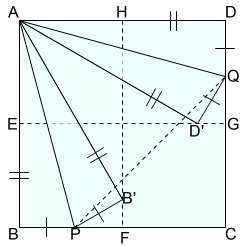証明1 \(△ABP\) と \(△AB’P\) ついては，Aを中心として半径ABの円を描くようにABの長さを移し，HFとの交点をB’としています。
その位置で折り目APを入れています。
\(△ADQ\) と \(△AD’Q\) についても同様です。
EGとの交点をD’とし，その位置で折り目AQを入れています。

\(△ABP\) と \(△AB’P\) において
\(AB=AB’,BP=B’P,∠ABP=∠AB’P=∠R\) より，二辺挟角が等しいので
\(△ABP\equiv △AB’P\)

同様に，\(△ADQ\) と \(△AD’Q\) において
\(AD=AD’,DQ=D’Q,∠ADQ=∠AD’Q=∠R\) より，二辺挟角が等しいので
\(△ADQ\equiv △AD’Q\)

したがって，正方形の定義から\(AB=AD\) であることから，\[△ABP\equiv △AB’P\equiv △ADQ\equiv △AD’Q\]
頂点Aで頂点を共有する４つの三角形は，すべて合同です。

（２）正方形の一辺を底辺とする正三角形

\(△AB’D\) において
\(△ABP\equiv △AB’P\) なので，\(AB=AB’\)　頂点B’はADの垂直二等分線FH上にあります。
\(△AHB’\) と \(△DHB’\) において
\(AH=DH,∠AHB’=∠DHB’=∠R,B’H\)共通より，二辺挟角が等しいので
\(△AHB’\equiv △DHB’\)
よって，\(AB’=DB’\)
一方，\(□ABCD\)は正方形なので\(AB=AD=AB’\)
したがって，\(AD=AB’=B’D\)
３辺が等しいので，\(△AB’D\) は，正三角形といえます。
このことから，\(∠B’AD=60°\)
\[\begin{equation}\begin{split}∠PAB&=∠R-(∠B’AD+∠PAB’)\\&=90°-(60°+∠PAB’)\\&=30°-∠PAB\\2∠PAB&=30°\\∠PAB&=15°\end{split}\end{equation}\]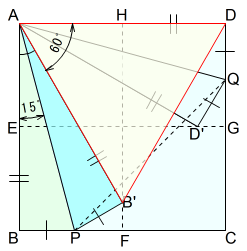 証明3
\(△ABP\equiv △ADQ\) から\[∠PAB=∠QAD=15°\]
証明2
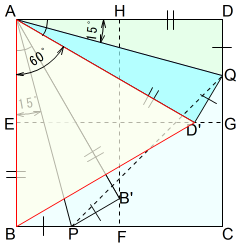
したがって，\[\begin{equation}\begin{split}∠PAQ&=∠R-(∠PAB+∠QAD)\\&=90°-15°\times 2\end{split}\end{equation}\]\[∠PAQ=60°\tag{1}\]
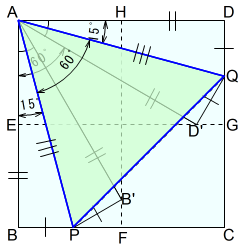証明4 \(△ABP\equiv △ADQ\) から\[AP=AQ\tag{2}\]
(1),(2)より，\(△APQ\) は，頂点Aの内角を60°とする二等辺三角形です。
二等辺三角形の両底角は等しいので，
\[\begin{equation}\begin{split}∠APQ&=∠AQP\\&=(180°-60°)\div 2\\&=60°\end{split}\end{equation}\]
\[∠PAQ=∠APQ=∠AQP=60°\]
すなわち，\(△APQ\) は，正三角形であるといえます。