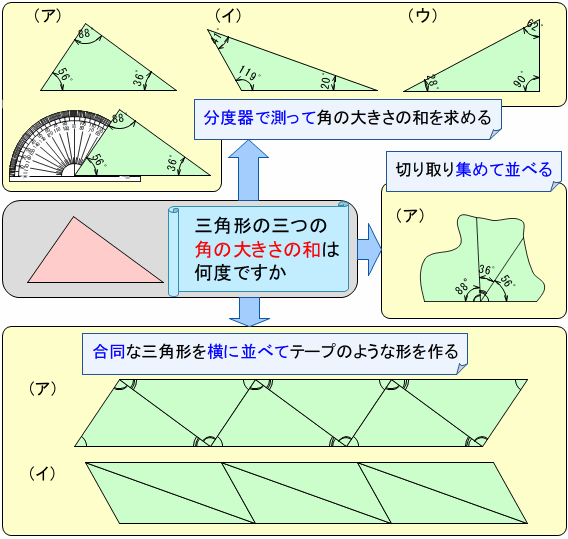
- 新学習指導要領の見方・考え方の具体例として,算数科「図形」領域では,数学的な見方・考え方の指導はどのようにすればよいのでしょうか。
- 「図形」領域の指導例として,第2学年「三角形と四角形」の指導では,三角形や四角形を構成する直線に着目し,それらの意味(概念)を理解できるようにします。
数学的な見方…三角形や四角形を構成する直線に着目する
数学的な考え方…三角形や四角形を構成する直線の数に着目して,類似点と相違点を考える
実践では,
1. 動物の家をつくる場面を設定し,直線で動物を囲む活動で構成要素の直線に気付くようにします。
2. できた形を2つに仲間分けする活動で,類似点・相違点を観察し直線の数に着目する数学的な見方・考え方を学びます。
3. さらには,図形を三角形と四角形の約束に基づいて,弁別する活動をします。演繹的に説明する場面です。
これらの活動を通して,三角形と四角形の理解を深めていくことがねらいです。
1 算数科の見方・考え方
新学習指導要領では見方・考え方が明示されました。
算数科・数学科の特質に応じた見方・考え方は,数学的な見方・考え方です。
「数学的な見方・考え方」は,
算数の学習において,どのような視点で物事を捉え,どのような考え方で思考をしていくのかという,物事の特徴や本質を捉える視点や,思考の進め方や方向性を意味します。
「数学的な見方・考え方」のうち「数学的な見方」については,
「事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること」です。
また,「数学的な考え方」については,
「目的に応じて数,式,図,表,グラフ等を活用しつつ,根拠を基に筋道を立てて考え,問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら,統合的・発展的に考えること」です。
小学校算数科の数学的な見方・考え方の例が,下記のように示されています。
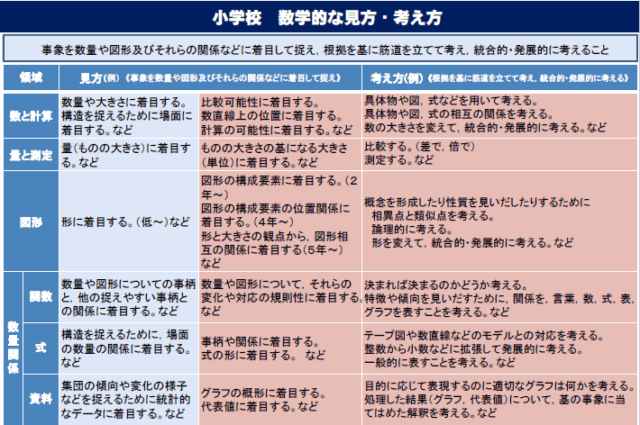
[1]文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2p5「数学的な見方・考え方」平成28年5月24日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
2 数学的な見方・考え方の具体例
(1)図形領域のねらい
新学習指導要領における算数科図形領域のねらいは,次の三つです。
・ 基本的な図形や空間の概念について理解し,図形についての豊かな感覚の育成を図るとともに,図形を構成したり,図形の面積や体積を求めたりすること
・ 図形を構成する要素とその関係,図形間の関係に着目して,図形の性質,図形の構成の仕方,図形の計量について考察すること。図形の学習を通して,筋道立てた考察の仕方を知り,筋道を立てて説明すること
・ 図形の機能的な特徴のよさや図形の美しさに気付き,図形の性質を生活や学習に活用しようとする態度を身に付けること
小学校学習指導要領解説算数編「第2章 算数科の目標及び内容B図形(1)「B図形」の領域のねらい」[ONLINE]https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf(cf.2020-06-09)
(2)図形領域の数学的な見方・考え方
図形領域における数学的な見方・考え方は,図形を構成する要素,それらの位置関係や図形間の関係などに着目して捉え,根拠を基に筋道を立てて考えたり,統合的・発展的に考えたりすることです。
具体的には,次のようです。
数学的な見方
・ 形に着目する
・ 図形の構成要素に着目する
・ 図形の構成要素の位置関係に着目する
・ 形と大きさの観点から,図形相互の関係に着目するなど
数学的な考え方
概念を形成したり性質を見いだしたりするために
・ 相異点と類似点を考える
・ 論理的に考える
・ 形を変えて,統合的・発展的に考えるなど
(3)第2学年「三角形と四角形」の数学的な見方・考え方
第2学年図形領域平面図形の「三角形と四角形」の指導では,
三角形や四角形を構成する直線に着目しながら,三角形と四角形の図形について理解できるようにします。
具体的には,3本の直線で囲まれた図形を三角形,4本の直線で囲まれた図形を四角形ととらえられるようにします。
したがって,
・ 数学的な見方:三角形や四角形を構成する直線に着目すること
・ 数学的な考え方:三角形や四角形を構成する直線の数に着目して,類似点と相違点を考えること
となります。
追記2018年4月25日 小学校学習指導要領(平成29年3月)
B(1) 三角形や四角形などの図形
(1) 図形に関わる数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 三角形,四角形について知ること。
(イ) 正方形,長方形,直角三角形について知ること。
(ウ) 正方形や長方形の面で構成される箱の形をしたものについて理解し,それらを構成したり分解したりすること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 図形を構成する要素に着目し,構成の仕方を考えるとともに,身の回りのものの形を図形として捉えること。
※ 図形を構成する要素に着目するとは,図形を捉える際に辺や頂点,面,直角といったものに着目すること。
構成の仕方を考えるとは,例えば,三角形を構成するためには3本の直線を用いる,また,それらのうち2本で頂点を構成する,というように,図形を構成する要素に着目し構成の仕方に見通しをもつこと。
※ 文部科学省「小学校学習指導要領第2章各教科第3節算数」平成29年3月[ONLINE]https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf(参照2020-06-09)
3 指導の実際
(1)既習内容
児童は,第1学年で,ものの形を認めることができています。
児童の身の回りにあるタイルや敷石の敷き詰めなどの具体物の中から,形のみに着目して,さんかく,しかく,まるなどの形を見付けています。
これは,数学的な見方です。
また,形の特徴をとらえることができています。
・ さんかくやしかくは,まると比べてかどがある
・ さんかくのかどは,三つある
・ さんかくとしかくを比べると,かどの数がちがう
といった形状の特徴をとらえることができています。
着目する構成要素として,かどやかどの数に目を向けています。
そこで,第2学年では,「さんかく」や「しかく」ではなく,約束に基づく「三角形」や「四角形」を学びます。
(2)学習活動1「動物を直線で囲む」
【構成要素の直線に着目する活動】
単元の導入では,動物の家をつくる場面です。
算数的活動とするために,「動物の家をつくろう」という目的意識がもてるように場面づくりをします。
草原に動物がいます。その動物の周りには,三角形や四角形の頂点に当たる部分がポイントされています。
【活動1】「点と 点を 直線で つないで どうぶつを かこみましょう。」
児童は,鉛筆と定規で直線をひき,動物を囲みます。
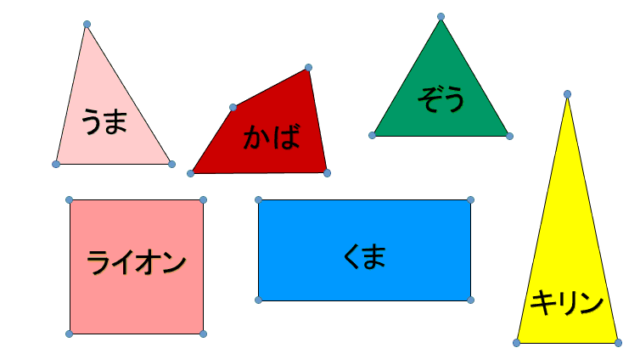
直線で動物を囲む活動を通して,児童は図形の構成要素である点や直線に意識が向くようにします。
この直線と点は,三角形と四角形の構成要素です。
この活動によって,三角形と四角形の構成要素である直線に着目できるようにします。
また,ここでは,「直線」で囲まれた図形をつくること,つないでかこむ(閉じた図形)であることを明確にして活動できるようにすることが大切です。
(3)学習活動2「できた形を2つに仲間分け」
【類似点・相違点を考え,直線の数の違いに着目する数学的見方に気付く活動】
【活動2】「できた 形を 2つの なかまに 分けましょう。」
活動1の際に,「同じ形」「一緒だ」「仲間だ」などの児童の気付きをとらえておきます。
その児童の気付きを基に,児童の意識の流れをつなぎながら,活動2の目的意識につなぐことが大切です。
ここではすでに「動物の家」という要素は捨象して,「形」を考察の対象にします。
活動1でつないだ直線に着目して,仲間分けをします。
しかも,2つに分けます。
直線に着目する見方で,2つに分けることを考えます。
類似点・相違点を考えると,囲まれている直線の本数の違いに目が向くようになります。
【問い】「似ているのは,どれかな」「どこが似ているかな」
【問い】「違うのは,どれかな」「どこが違うかな」
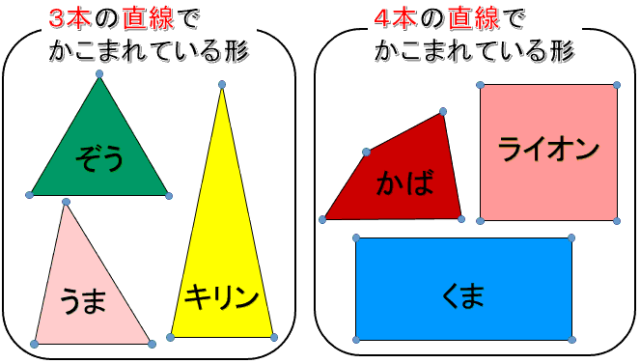
この仲間分けの活動を通して,3本の直線で囲まれている形を三角形といい,4本の直線で囲まれている形を四角形ということを約束します。
厚紙を裁断機で切ったようなまっすぐな直線の三角形や四角形を児童に触らせるなどして,直線で囲まれている形の実感がもてるようにすることが大切です。
(4)学習活動3「三角形と四角形の判断(弁別)」
【演繹的に考え根拠に基づいて説明する活動】
【活動3】「三角形や,四角形をみつけましょう。また,そのわけを いいましょう。」
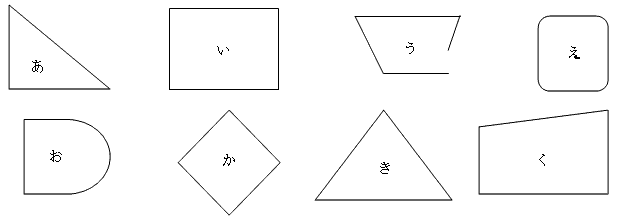 ここでは,それぞれの図形が,三角形四角形の約束に基づいているかどうかを考え判断する活動です。
ここでは,それぞれの図形が,三角形四角形の約束に基づいているかどうかを考え判断する活動です。
【問い】「これは,三角形(四角形)かな」「どうして三角形(四角形)なのかな(といえるのかな)」「どうして三角形(四角形)でないのかな(といえないのかな)」
C:「あ」は,3本の直線で囲まれているから三角形です。
C:「う」は,囲まれていないから四角形ではありません。
約束に基づいた説明ができる必要があります。
演繹的に考える場面です。
これらの活動を通して,三角形と四角形の理解を深めていくことがねらいです。
(5)学習のまとめと振り返り
終末の学習のまとめでは,
1. 三角形と四角形が直線で構成されていること
2. 類似点,相違点は,直線の数であること
3. 直線の数に着目すると,三角形と四角形に仲間分けできること
4. 3本の直線で囲まれている図形が三角形,4本の直線で囲まれている図形は四角形であること
5. 約束に基づいて判断すると,三角形と四角形が見分けられること
6. 三角形と四角形は,まっすくな直線でつくられ頂点はとがっており,しかも,閉じた図形であること
1,2は,図形についての解決につながった数学的な見方を振り返ります。
3,4は,図形を観察した結果から得られた知識を確かめます。
5は,演繹的な数学的な考え方です。確かな根拠をもって論理的に説明する方法を振り返ります。
6は,演繹的に考え結果から得られた深い学びです。深く学ぶよさを味わえるようにします。
このように,指導場面の数学的な見方・考え方を明確にして,授業を設計していくことが大切です。
参考文献
文部科学省小学校学習指導要領解説算数(1)第1章~第2章(平成20年6月)[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf(参照2017/05/16)
文部科学省小学校学習指導要領解説算数(2)第3章~第4章(平成20年6月)[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf(参照2017/05/16)
第2学年「三角形と四角形」の指導では,三角形や四角形を構成する直線に着目し,それらの意味(概念)を理解できるようにします。
数学的な見方…三角形や四角形を構成する直線に着目すること
数学的な考え方…三角形や四角形を構成する直線の数に着目して,類似点と相違点を考えること
実践では,
1. 動物の家をつくる場面を設定し,直線で動物を囲む活動で構成要素の直線に気付くようにします。
2. できた形を2つに仲間分けする活動で,類似点・相違点を観察し直線の数に着目する数学的な見方・考え方を学びます。
3. さらには,図形を三角形と四角形の約束に基づいて,弁別する活動をします。演繹的に説明する場面です。
これらの活動を通して,三角形と四角形の理解を深めていくことがねらいです。