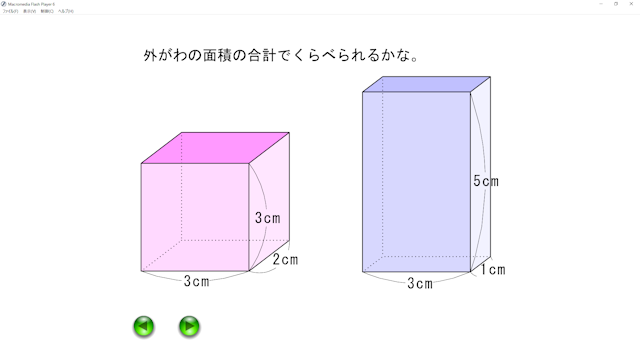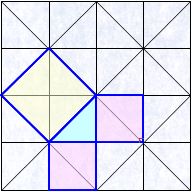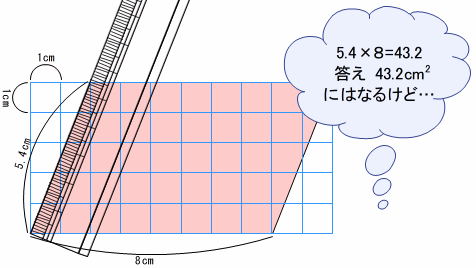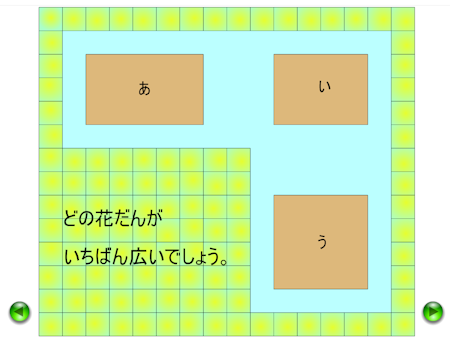
- 小学校算数科「測定」の指導は，どのようにすればよいのでしょうか。
- 測定の内容は，量の把握とその測定の方法の理解です。
長さ，広さ，かさ，重さという保存性と加法性のある量についての「測定」の指導では，一般に，直接比較，間接比較，任意単位による測定，普遍単位による測定という４段階の比較・測定の学習活動を設定します。
指導の際には，測りたい量は何か，実感をもって理解できるようにします。また，量の大きさを比べる際には，場面や目的及び身の回りのものの特徴に応じて量の大きさの比べ方を見いだすことができるようにします。さらに，測定領域の学習を日常生活に積極的に活用することで，算数への関心を高め，算数を主体的に学ぶ態度の育成へとつなげることが大切です。
１ 測定領域の指導のねらい
（１）領域構成
① ５領域構成
小学校学習指導要領（平成29年告示）における算数科の内容は，以下の五つの領域で構成されます。
Ａ 数と計算
Ｂ 図形
Ｃ 測定 （第１〜３学年）
Ｃ 変化と関係 （第４〜６学年）
Ｄ データの活用
これらの領域の区分けは，数・量・図形に関する内容とそれらの考察の方法を基本とする領域（Ａ数と計算，Ｂ図形，Ｃ測定），事象の変化や数量の関係の把握と問題解決への利用を含む領域（Ｃ変化と関係），不確実な事象の考察とそこで用いられる考え方や手法などを含む領域（Ｄデータの活用）として設定したものです。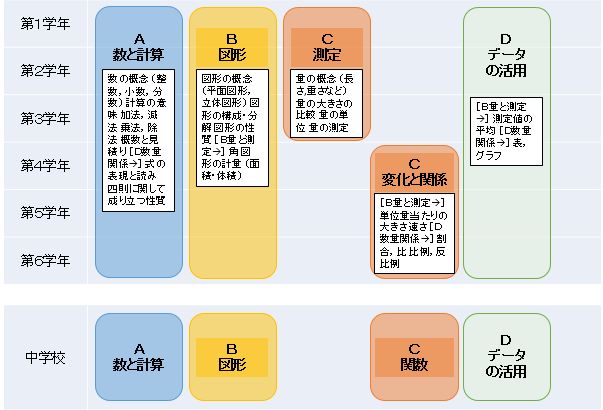
② 測定の内容の概観*
測定領域の内容の骨子を簡略に述べると，量の把握とその測定の方法の理解といえます。併せて，筋道を立てて考えること，数学的に表現すること，数学的に伝え合うことができるようにします。
身の回りにある二つのものを比較する場合，比較対象となるものの属性(例えば，長さや重さなど)に着目し，その属性について数値化して表すことがあります。
算数科で学ぶ量の把握における測定とは，幾つかのものを比較する必要から，ものの特徴を捉えてそれを測り取り，数値化して表すことです。
この意味で，量の把握における測定とは，ものの属性に着目し，単位を用いて量を捉え，その単位で測り取った数値に対応させることです。
例えば，ものの重さは，「重さ」という属性で単位とする大きさを決めて測定し数値化できます。
数学的には，量の測定とは，ものの集合から実数の集合への関数であるとみることができます。
このようなものの属性の数値化においては，ものの属性を直接比較すること，大小関係の推移律に基づいて行われる間接比較，そして任意の単位を設定して測定した結果の比較，そして普遍単位による測定という過程を通して，測定の意味についての学習を行います。
（２）指導のねらい*
（１）身の回りの量について，その概念及び測定の原理と方法を理解するとともに，量についての感覚を豊かにし，量を実際に測定すること
（２）身の回りの事象の特徴を量に着目して捉え，量の単位を用いて的確に表現すること
（３）測定の方法や結果を振り返って数理的な処理のよさに気付き，量とその測定を生活や学習に活用しようとする態度を身に付けること
（３）数学的な見方・考え方に着目した内容*
① 量の概念を理解し，その大きさの比べ方を見いだすこと
② 目的に応じた単位で量の大きさを的確に表現したり比べたりすること
③ 単位の関係を統合的に考察すること
④ 量とその測定の方法を日常生活に生かすこと
（４）領域の数学的な見方・考え方*
身の回りにあるものの特徴などに着目して捉え，根拠を基に筋道を立てて考えたり，統合的・発展的に考えたりすること
２ 保存性と加法性のある量
長さ，面積，体積，重さ，角の大きさなどの基本的な量（外延量）は，量の保存性と加法性があります。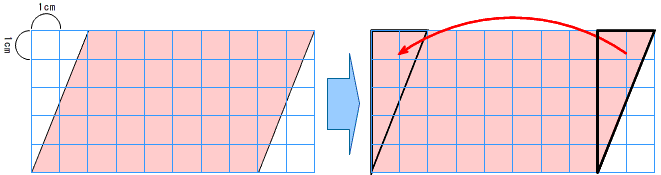
・ 量の保存性…ものの形を変形したり，幾つかに分割したり，位置を動かしたりしても，そのものの量の大きさは変わらない。
・ 量の加法性…測定したい２つのものを合併したときの量が，それぞれのものの量の加法によって計算できる。
重さなどは加法性が成り立つ量であり，外延量といいます。
加法性の成り立たない量もあります。例えば，温度です。
30度のお湯に40度のお湯を足すと，30＋40 で70度，とはなりません。ヤカンに，15度の水をコップで順に，１杯，２杯，…，と加えても15°ずつ温度は上昇しません。30度のお湯の温度を5度上げると35度とはなりますが，5度の水を加えたわけではありません。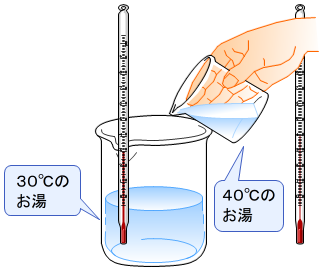
このような加法性が成り立たない量を内包量といいます。他にも，速度，密度，濃度などの内包量があります。
外延量には，量を数値化する共通の方法がありますが，内包量には共通した方法がなく，色々な方法を使います。
量の保存性等のある基本的な量の測定の指導では，一般に，４段階の比較・測定の学習活動を設定します。直接比較，間接比較，任意単位による測定，普遍単位による測定という段階です。
それらの数学的活動を通して，基準となる量を決めてそのいくつ分かで表して数値化するという測定の仕方を児童が見出して身に付けられるようにします。
３ 比較・測定の段階
（１）直接比較
直接比較では，比べたいものの２つの大きさを，直接重ねるなどして比べます。
移動できるものを比べる場合には，これらを動かして，並べて置いたり重ねたりして比べます。
例えば，長さの比較です。
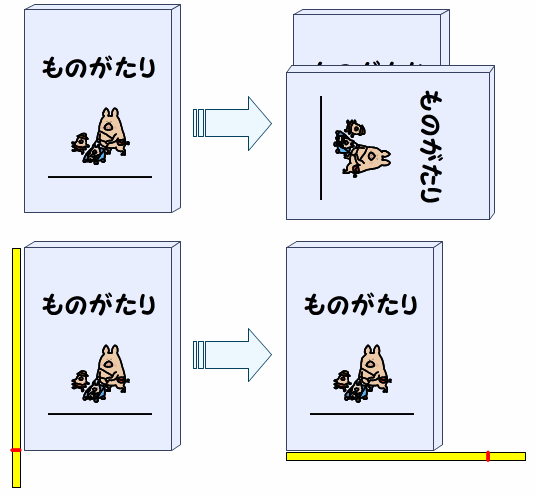
２冊の本の縦の長さを比べるとき，傾けて置かれた本は正しく比べられません。本立てにきちんと本を並べると，本の上の位置で縦の長さが比べられます。上の位置が高い方が，縦の長さが長いといえます。
このように，直接比較は，比べたい２冊の本を直接並べたり重ねたりして比べます。その際，本立てに揃えて置き，下を揃えるなど一方の端を揃えて比べる必要があります。
（２）間接比較
間接比較では，比べたいものの２つの大きさを，それと等しい別のものに置き換えて，間接的に比べます。
比べるものが移動できない，目の前にない，時間とともに過ぎ去るようなとき，一方の量または両方の量を第３のものに置き換えて，写し取った量を使って直接比較します。
これは，媒介物を用いた間接的な比較です。
例えば，折り曲げられない物語の本で１冊しかないなどの場合は，直接重ねて比べることは困難です。
しかし，紙テープを使うと長さが比べられます。
まず，物語の本の縦に合わせて，一方の端を揃えて他方の端に印を入れます。
次に，紙テープを物語の本の横に端を揃えて合わせます。
物語の本の横の長さが，印を入れたところより内側に含まれていれば，縦の方が長いといえます
このような直接比較や間接比較を通して，具体的なものの属性のうち，比べようとしている量は何なのかが明確になり，その量についての理解が深まります。
（３）任意単位による測定
任意単位による測定では，比べたい２つのものの大きさを，それと同種の量のいくつ分という数値に置き換えて比べます。
大きさがどれだけかを示すために，量の大きさを数で表す量の「数化」を行います。
数化するために，測定するものと同種な適当なものを単位に決め，そのいくつ分かで大きさを表します。
これは，単位は任意に決められることから，任意単位による測定といいます。
例えば，任意単位としてクリップを利用して，本の縦と横の長さを測定します。
本の縦にはクリップが８個並び，横にはクリップが６個並びました。
クリップの数の多い縦の長さの方が，横の長さよりクリップ２個分長いといえます。
第１学年の授業では，任意単位とするものは，手を開いた長さ，鉛筆や消しゴムの長さなど，子どもの身近なものを利用します。
このように数値化することで，大きさの違いを明確に数を使って表して比べられるようになります。
（４）普遍単位による測定
人によって使用する単位が違えば，せっかく測定しても大きさを正しく伝え合うことができません。
社会では，基にする単位の大きさが誰にも的確に分かる必要があります。
そのため，基にする単位として普遍的な法定単位を用いることになります。
この単位による測定が，「普遍単位による測定」です。
指導では，多くの人と伝え合えるように共通な単位が必要になるという単位の必要感がもてるようにします。
例えば，離れたところにいるＡさんとＢさんが，自分の持つ本の縦の長さを互いに比べようとしています。
測定してみると，Ａさんは鉛筆２本分の長さ，Ｂさんは鉛筆３本分の長さということが分かりました。
ところが，基準とした鉛筆長さがお互いに分かりません。単位が異なる可能性があるので単純には比較はできません。
このような不都合な状況を子どもに経験させることで，普遍単位による測定の必要性を感じことができるようにすることが大切です。
量の普遍単位としては，
第２学年：長さの単位ミリメートル（mm），センチメートル（cm)，メートル（m），かさの単位ミリリットル（mL），デシリットル（dL），リットル（L），時間の単位（日，時，分）
第３学年：長さの単位（キロメートル（km）），重さの単位（グラム（ｇ），キログラム（kg）），時間の単位（秒）
を指導します。なお，単位については，日本では計量法という法律によって，国際的には「国際単位系」というルールによって定められています。
４ 日常生活に生かす*
測定領域は，身の回りの量の大きさについて学習するため，日常生活の多くの場面で生かすことができます。例えば，次のようなことです。
・ 時刻と時間の読みを基に，日常生活における時間の使い方についての計画を立てたり，生活時間の目安をつくったりすること
・ 長さの見当付けを基に，本棚の1列に本をだいだい何冊程度収納することができるか見積もること
・ 身近な具体物の長さを基に，身の回りのものの大きさを概測すること
・ 商品の表示等で示されている単位等に関心をもったり，その単位の仕組みを長さやかさの単位と関連付けて捉えたりすること
このように，測定領域の学習を日常生活に積極的に活用することで，算数への関心を高め，算数を主体的に学ぶ態度の育成へとつなげることが大切です。
５ まとめ
長さ，重さなどの基本的な量（外延量）は，量の保存性と加法性があります。
量の保存性等のある基本的な量の測定の指導では，一般に，直接比較，間接比較，任意単位による測定，普遍単位による測定という４段階の比較・測定の学習活動を設定します。
指導の際には，量りたい量は何か，比べようとしてる対象はどのようなものなのかを実感をもって理解できるようにします。
また，量の大きさを比べる指導においては，場面や目的及び身の回りのものの特徴に応じて量の大きさの比べ方を見いだすことができるようにします。このことは，目的に応じて量の大きさの比べ方を柔軟に選択し，学習した方法を活用する資質・能力の育成を目指す上で特に重要です。
測定の指導内容は，単元の学習活動に類似性があります。系統上の既習内容である量の意味や測定の意味の学びを生かす展開が大切です。
引用(*)・参考文献
文部科学省小学校学習指導要領（平成 29 年告示）解説 算数編[ONLINE]https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf（参照2020-06-19）
