数，数字，数詞の違いと数が分かること

「数が分かる」とは，どういうことなのでしょうか。

数が分かるとは，数の概念が理解できることです。数字がかけたり数詞が言えたりしても，数を理解したとはいえません。
・　数字は，数を表現する記号です。アラビア数字やローマ数字などがあります。
・　数詞は，数の読み方です。フランス語では「アン，ドゥ，トロワ」，ドイツ語では「アインス，ツヴァイ，ドライ」，日本語では「いち，に，さん」など，国によって違います。
では，数とは何でしょうか。数は，目に見えず，物を見せて示すことができません。
ものの集合に一対一の対応を付けて抽象したもの，対等な集合に共通な性質が数の概念です。それに名前を付け数字と数詞を約束します。








１　数が分かるとはどういうことか

小学校第１学年で，「１，２，３，…」という数を学びます。入学する前から「１，２，３」と言えたり，数字がかけたりする子どももいます。そのような子どもでも，本当に数を理解しているかは分かりません。
本当に「数が分かる」とは，どういうことなのでしょうか。分かったといえるのは，どんなときなのでしょうか。
指を１本，２本，３本と立てて，それに対して「１，２，３」と言えることは必要です。あるいは「１，２，３」と数字がかけることも必要です。
しかし，本当に数が分かったといえるのは，数の概念が理解できたときです。
このような数の理解をテーマとするとき，数と数字と数詞の違いを確かめておく必要があります。

２　数字とは何か

（１）数字の種類

まず，数字について考えます。
数字は，数を表現するための文字あるいは記号です。数字には以下のようなものがあります。

アラビア数字	0	1	2	3	4	5	6	7	8	9
インド数字	٠	١	٢	٣	٤	٥	٦	٧	٨	٩
ローマ数字		I	II	III	IV	V	VI	VII	VIII	IX
ギリシャの数字		α’	β’	γ’	δ’	ε’	ϛ’	ζ’	η’	θ’

他にも，日本で使われる漢数字，アルメニア数字，ヘブライ数字，タイの数字 などがあります。
ここでは，見かけることのあるローマ数字と，日常的に使う漢数字，アラビア数字を取り上げます。
その他の使用される記号などの詳細は，ウィキペディア「数字」の項目に参考にされてください。
参考：ウィキペディア「数字」https://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%97

（２）ローマ数字の記号と表記法

ローマ数字は，時計の文字盤に使われることがあります。また，クイーンエリザベスⅡ世号などと固有名詞や伝統的なものを呼ぶときなどに使う数字です。
ローマ数字は，Ｉ，Ｖ，Ｘ，Ｌ，Ｃ，Ｄ，Ｍの７文字で数を表します。それぞれ，１，５，１０，５０，１００，５００，１０００の数を表します。
ローマ数字は表記法が工夫されており，基本的には文字を増やして表します。
１はＩ（Ｉが１つ），２はⅡ（Ｉが２つ），３はⅢ（Ｉが３つ）です。
１０はＸ，２０はＸＸ，３０はＸＸＸです。
１００はC､２００はＣＣ，３００はＣＣＣ，
１０００はＭが１つ，２０００はＭＭ（Ｍが２つ）と言う具合です。

例えば，ＭＭＣＸＩＩと表記すれば，２，１１２を表します。
ただし，同じ文字を４つ以上並べられないとしているため，４を表すのに，IIIIとはしません。４は，ＩＶと表記します。時計の文字盤については慣習上例外的にIIIIを使うようです。

小さい数字が前にある場合は，引き算をします。
Ｖ（５）－Ｉ（１）＝ＩＶ（４）
４０であれば，ＸＬと表します。
Ｌ（５０）－Ｘ（１０）＝ＸＬ（４０）
９０であれば，ＸＣと表します。
Ｃ（１００）－Ｘ（１０）＝ＸＣ（９０）
９００であれば，ＣＭと表します。
Ｍ（１０００）－Ｃ（１００）＝ＣＭ（９００）

ローマ数字は，このような表記方法を用いて数を表しています。ちなみに，ローマ数字には「０」はありません。

（３）漢数字の文字と表記法

漢数字についてですが，これは日常的に使っている数字なので十分ご承知かと思います。
１から９までの数について，一，二，三，四，五，六，七，八，九の漢字が割り当てられています。零もありますが，漢数字による表記では通常必要としません。そして，位を表す漢字として，十，百，千，万，億，兆などがあります。
この位の文字については，江戸時代の吉田光由(1598-1673)が著した塵劫記(1627年初版)に詳しく記されています。
漢数字では，これらの１から９の数を表す漢字と位を表す漢字を組み合わせて数を表しています。
吉田光由 編「新編塵劫記上巻　第一大数の名の事」出版者古典数学書院昭和10写本国立国会図書館インターネット公開（保護期間満了）[ONLINE]http://dl.ndl.go.jp/info:ndljp/pid/1129154/6(2017/6/1)

（４）アラビア数字の記号と表記法

アラビア数字は，算用数字と呼ばれ，現在算数や数学で使っている数字です。アラビア数字は，インド数字に起源がある十進位取り記数法で表す数字です。０から９までの１０種類の数字を使います。
整数は十進位取り記数法を用いて表されますが，この記数法は，位の位置によって大きさを表せるという優れた方法です。それによって簡潔に分かりやすく数を表したり，数の大小を比較したりできます。

これまで見てきたように数字は，それぞれの国や地域でつくられた数を表す記号や文字です。
同じ数を表すのに数字は違います。数字は，数そのものを表しているものではありません。しかし，数そのものを表さないからと言って不要というわけではありません。

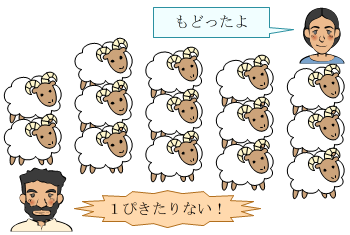
数は生活に必要であり，それを使って必要な情報を伝え合う必要があります。そのため数をどう表すかについて共通理解を図る必要があります。それを基に数について考えるからです。
このように，数について伝え合うためには，数を表す記号や文字がかけたり読めたりすることが必要となります。

３　数詞とは何か

次に，数詞を考えます。
数詞とは，数を表す言葉，数の読み方です。言葉であることから国や地域でよって違います。
数字で，１，２，３，４，５と書くと，読み方は国によって違います。
フランス語では，
１ un,une アン，ユヌ ，２ due(X) ドゥ，３ trois トロワ ，４ quatre キャトル，５ cinq サンク
ドイツ語では，
1 eins アインス，2 zwei ツヴァイ，3 drei ドライ ，4 vier フィーア，5 fünf フュンフ
英語では，
1 oneワン，2 two トゥー ，3 three スリー ，4 four フォー ，5 five ファイブ
中国語では，
1一イー，2二アァ，3三サン，4四スゥ，5五ウゥ
となります。
日本語では，「いち」「に」「さん」「し」「ご」です。

オーストラリア人から「日本の人口は何人ですか」とたずねられたことがあります。１億２０００万人と答えたいのですが，英語での読み方が分かりません。手元に紙もありません。頭の中で，thousand，million，billionと数えます。thousandは千の位，millionは百万の位，すると，billionは何の位か?と，冷や汗をかいた経験があります。
振り返るに，日本の数の読み方は４桁ごとに，英語では３桁ごとに変わります。万，億，兆とthousand，million，billionが対応すれば，比較的容易に読み替えることができます。しかし，日本語と英語では数の読み方の仕組みに違いがあり読み方の換算が必要です。

数と数字と数詞の違いをまとめると，数字は数を表す記号，数詞はその数の読み方であるということができます。

４　数とは何か

では，数とは何でしょうか。
数は，目に見えず，物を見せてこれですと，示すことができません。
・（　１，１，１　)
・（　■，■，■　)
・（　ａ，ａ，ａ　)
・（　車，車，車　)
・（　ケーキ，ケーキ，ケーキ　)
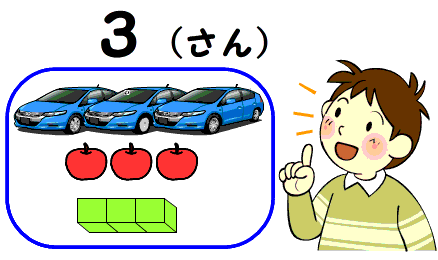
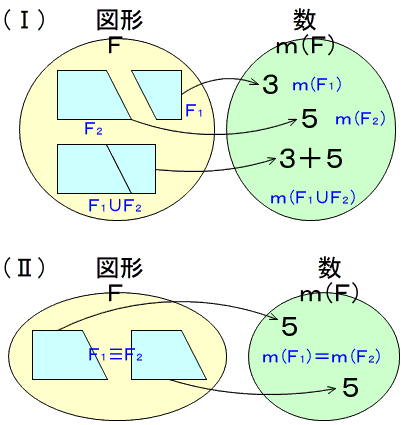
これらに共通するものは何でしょうか。「１，１，１」，「車，車，車」，「ケーキ，ケーキ，ケーキ」などのどの集合も要素の数が同じである対等な集合です。
それぞれに一対一の対応を付けて抽象したもの，共通な性質が，数の３の概念です。
それに３と言う名前を付けます。
そして，「３」とかき「さん」とよみます。
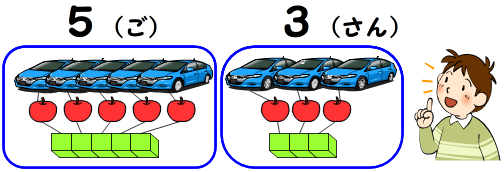実際の指導では，ものとものとを対応させることによって，ものの個数を比べるなどの活動から始めます。
やがて，その個数を正しく数えたり，数えたものの個数を数字で表したりすることができるようにします。
また，こうした活動を通して，数の大小や順序を知り，次第に数の意味，100までの数の構成について理解できるようにすることが第１学年のねらいの一つです。

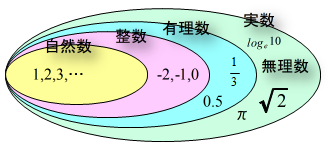自然数，整数，素数，有理数，無理数は，数の概念です。自然数⊂整数⊂有理数⊂実数。なお，小数と分数は，有理数を表すのに使われる表現形式です。
このように，算数の指導の中心の一つが，この数の概念に関わる内容の指導です。
見えない数を，一人一人の子どもが具体的事象の中から自分で抽象して理解していくものです。
それを理解できるようにすることが，算数の授業のねらいの一つです。

５　まとめ

数が分かるとは，数の概念が理解できることです。数字がかけたり数詞が言えたりしても，数を理解しているとは言えません。
数字は，数を表現するための記号です。アラビア数字やローマ数字などがあります。
数詞とは，数の読み方です。フランス語では「アン，ドゥ，トロワ」，ドイツ語では「アインス，ツヴァイ，ドライ」，日本語では「いち，に，さん」など，国や地域によって違います。
数は，目に見えず，物を見せてこれですと，示すことができません。ものの集合に一対一の対応を付けて抽象したもの対等な集合に共通する性質が，数の概念です。それに名前を付け数字と数詞を約束します。
算数の指導の中心の一つが，この数の概念でありそれを理解できるようにすることが，算数の授業のねらいの一つです。

参考文献
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）