- コピー用紙などのA判・B判規格紙から無理数を見つけるには，どのように操作してどこの長さを見るとよいのでしょう。
- A判の短辺と長辺，B判の短辺と長辺の４つの長さの比は一定であり，無理数を含みます。
A判とB判紙の並べ方を工夫したり折ったりして，直角三角形の長さに着目し三平方の定理を基にして，\(\sqrt{n},n\in A=\{2,3,4,5,6,7,8,9,10\}\)を見出すことができます。
１ A判とB判の規格
（１）規格の原則
コピー用紙などA判とB判と呼ばれる紙のサイズには，決まりがあります。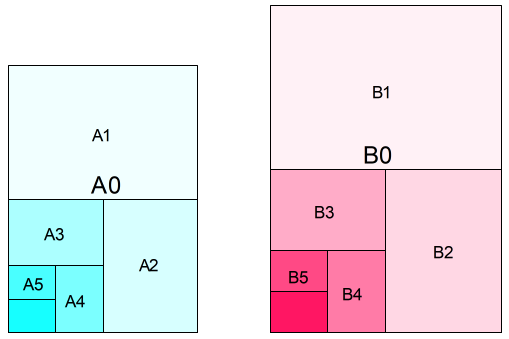
紙の２等分を繰り返しそれらが互いに相似となるように，紙のサイズが決まっています。
具体的には，A判，B判規格の紙は，どれも形が同じです。長方形の短辺と長辺の長さの比が \(1:\sqrt{2}\) の相似形です。
また，B判の面積はA判の面積の 1.5 倍です。A判についてはA0判の面積を \(1m^2\)，B判についてはB0判の面積を \(1.5m^2\) とし，２等分と相似の原則に基づいて，各判各辺の長さを決めています。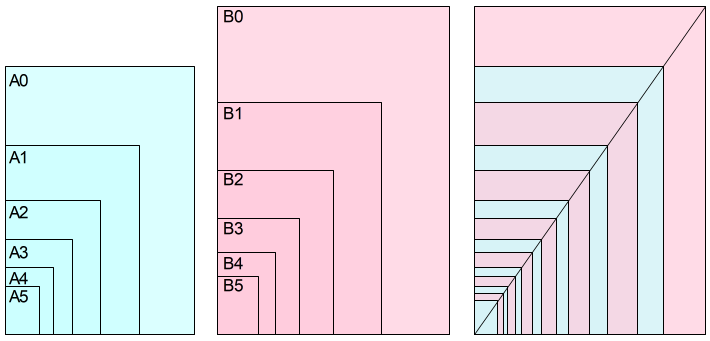
上記の詳しい内容は，別稿「A判・B判紙の長辺と短辺の比は 1:√2」*1を参照ください。
なお，この「判」の呼称に関連して「シリーズ，列」という呼称がありますが，本稿では，便宜的にA4判，A判などと一律に「判」を使用することとします。
さて，本稿では，A判とB判の辺の比を基にして，A判とB判の紙を操作して，\(\sqrt{n},n\in A=\{2,3,4,5,6,7,8,9,10\}\)を見出していきます。
（２）A判とB判の辺の比
上記の原則に基づいて各判の辺の長さが決められています。
ここでは，同番号のA判とB判の辺の比で表すこととします。ただし，A判の短辺を 1 とします。
例えば，A4判の短辺を 1 とすると，B4判の長辺は\(\sqrt{3}\)となります。
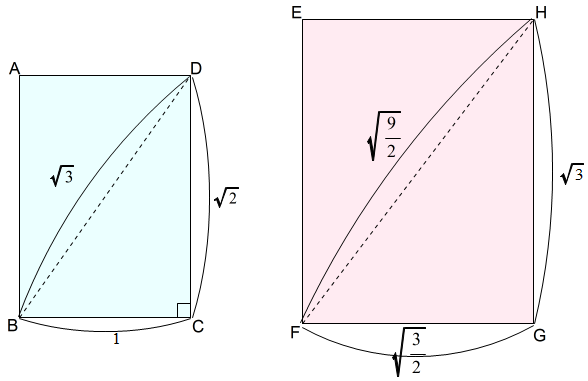
A4判の短辺を 1 とすると，同一番号のA判の短辺\(BC\)と長辺\(DC\)，B判の短辺\(FG\)と長辺\(HG\)の比は，次のようになります。
\[BC:DC:FG:HG=1:\sqrt{2}:\sqrt{\dfrac{3}{2}}:\sqrt{3}\tag{1}\]
(1)の詳細については，別稿「A判とB判の図形としての無理数の関係」で説明しています。また，実際に紙を折って確かめる方法も解説しています。
２ 無理数を作る
（１）\(\sqrt{5},\sqrt{6}\)を作る
\(\sqrt{2},\sqrt{3}\) は既に分かっています。A判の対角線が \(\sqrt{3}\) であることは，三平方の定理より証明できます。（※証明は別稿「A判とB判の図形としての無理数の関係」）
また，\(\sqrt{4}\) は，\(\sqrt{4}=2\) で無理数ではありません。
まず，\(\sqrt{5},\sqrt{6}\) から，見つけることを始めましょう。
なお，A判とB判は，図形として長方形であることを前提として以下の話を進めます。
下左図はA判を横向き，B判を縦向きにして，頂点B(頂点F)を揃えて重ねています。
このとき，\(BC=\sqrt{2},EF=\sqrt{3}\) 及び三平方の定理より \(EC=\sqrt{5}\) となります。
$$\begin{equation}\begin{split}BC^2+EB^2&=EC^2\\\sqrt{2}^2+\sqrt{3}^2&=EC^2\\EC^2&=5\\EC&=\sqrt{5}\end{split}\end{equation}$$
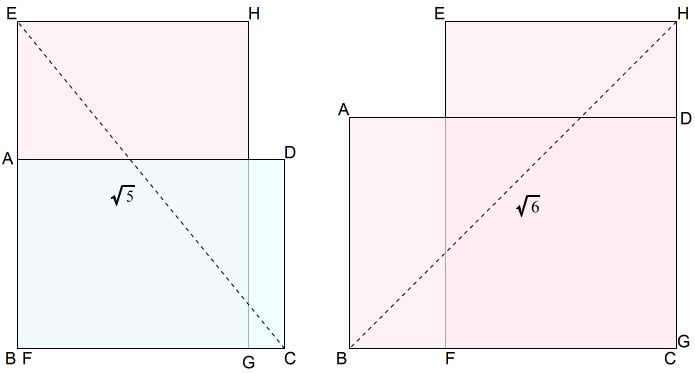
上右図は，B判二枚を頂点C(頂点G)を揃えて，図のように重ねています。
このとき，\(BC=HC=\sqrt{3}\) 及び三平方の定理より \(BH=\sqrt{6}\) となります。
$$\begin{equation}\begin{split}BC^2+HC^2&=BH^2\\\sqrt{3}^2+\sqrt{3}^2&=BH^2\\BH^2&=6\\BH&=\sqrt{6}\end{split}\end{equation}$$
（２）\(\sqrt{7}\)を作る
A判を二枚，B判を二枚用意します。隣接する判の一つ大きい紙を一枚ずつ用意してもよいです。
例えば，A4判とB4判をそれぞれ二枚ずつ計四枚を用意するのであれば，A3判とB3判をそれぞれ一枚ずつ計二枚を用意しても作ることができます。
A3判とB3判の場合では，それぞれ半分におって折り目をつけます。
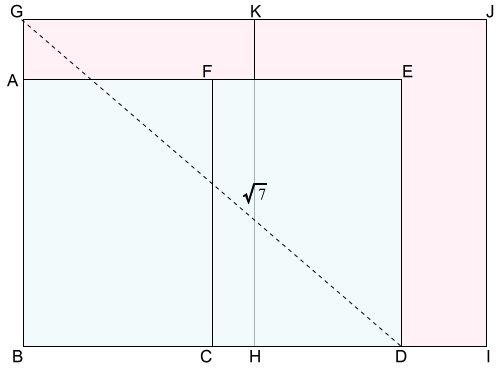上図では，A判二枚とB判二枚を長辺を合わせて，頂点Aに揃えて重ねています。
このとき，\(BC=CD=1,BG=\sqrt{3}\) 及び三平方の定理より \(GD=\sqrt{7}\) となります。
$$\begin{equation}\begin{split}BD^2+BG^2&=GD^2\\2^2+\sqrt{3}^2&=GD^2\\GD^2&=7\\GD&=\sqrt{7}\end{split}\end{equation}$$
（３）\(\sqrt{8}\)を作る
A判を四枚用意します。隣接する判の一つ大きい紙を二枚用意してもよいです。
例えば，A4判四枚であれば，それにかえてA3判二枚を用意してもよいです。
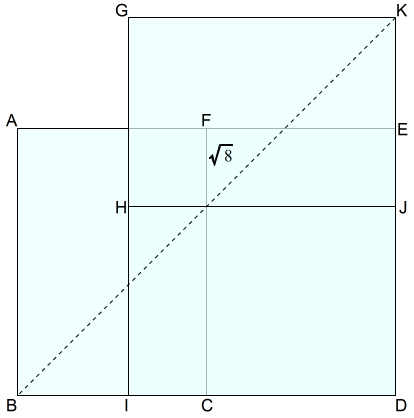上図は，A判を二枚ずつ縦向きと横向きにして，頂点Dに揃えて重ねています。
このとき，\(BD=KD=2\) 及び三平方の定理より \(KB=\sqrt{8}\) となります。
$$\begin{equation}\begin{split}BD^2+KD^2&=BK^2\\2^2+2^2&=BK^2\\BK^2&=8\\BK&=\sqrt{8}(=2\sqrt{2})\end{split}\end{equation}$$
３ \(\sqrt{n}\)を見出す
（１）A判三枚で見つかる無理数\(\sqrt{n}\)の長さ
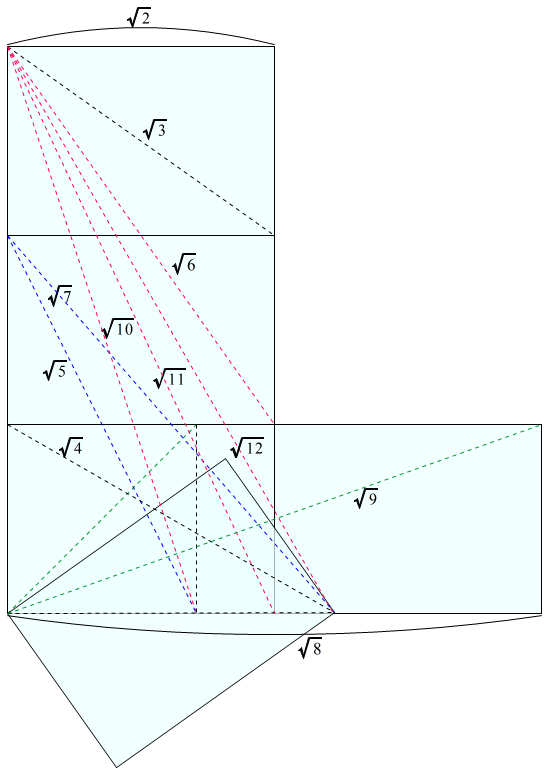
三枚のA判を使って図のように配置すると，\(\sqrt{2},\sqrt{3},\sqrt{4},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{9},\sqrt{10}\)を作ることができます。
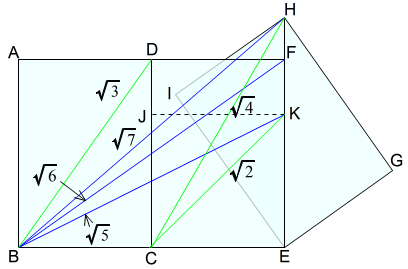上図では，A判二枚の長辺DCを重ねて，三枚目A判IEGHは，頂点Eを一致させ，A判DCEFの長辺FEにA判IEGHの対角線HEを重ねるようにします。
また，A判DCEFの辺CEを頂点Eを中心として，辺CEと辺FEが重なるように折り返します。点Cと重なった辺FE上の点を点Kとします。同様に点Eを折り返した点を点Jとします。
このとき，四角形JCEKは一辺が 1 の正方形です。
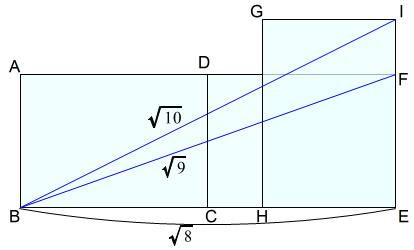上図では，A判二枚の短辺DCを重ねています。三枚目のA判GHEIの頂点Eを揃え，辺IEをA判DCEFの辺FEに，辺HEをA判DCEFの辺CEに重ねて配置します。
（２）\(\sqrt{n},n\in A=\{2,3,4,5,6,7,8,9,10\}\)
① \(\sqrt{2}\)
下図は，A判一枚の長方形です。
長方形の短辺の長さ 1 を辺AB及びDC上に移しています。
\(BF\)は，一辺を 1 とする正方形の対角線の長さです。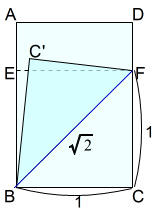
$$\begin{equation}\begin{split}BC^2+CF^2&=BF^2\\1^2+1^2&=BF^2\\BF^2&=2\\BF&=\sqrt{2}\end{split}\end{equation}$$
② \(\sqrt{3}\)
下図は，A判一枚の紙の長方形です。
\(BD\)は，A判の対角線の長さです。
また，\(\sqrt{3}\)は，B判の長辺の長さでもあります。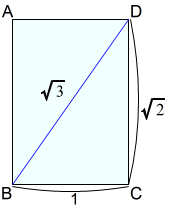
$$\begin{equation}\begin{split}BC^2+CD^2&=BD^2\\1^2+\sqrt{2}^2&=BD^2\\BD^2&=3\\BD&=\sqrt{3}\end{split}\end{equation}$$
③ \(\sqrt{4}\)
下図では，A判二枚を使っています。
A判ABCD,A判BEFCの長辺BCを重ねています。
A判ECFGは，A判ABCDの頂点Cと頂点を一致させ，A判ABCDの長辺CDにA判ECFGの対角線CGを重ねています。
\(BG\)は，A判の短辺と対角線を利用した長さです。
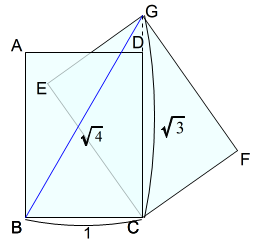$$\begin{equation}\begin{split}BC^2+CG^2&=BG^2\\1^2+\sqrt{3}^2&=BG^2\\BG^2&=4\\BG&=\sqrt{4}=2\end{split}\end{equation}$$
④ \(\sqrt{5}\)
下図は，A判二枚の長方形の長辺DCを重ねて並べています。
□JCEKは，一辺の長さが 1 の正方形です。
短辺二つ分と正方形の辺（短辺一つ分）を利用しています。
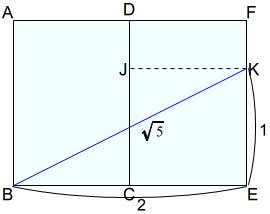$$\begin{equation}\begin{split}BE^2+EK^2&=BK^2\\2^2+1^2&=BK^2\\BK^2&=5\\BK&=\sqrt{5}\end{split}\end{equation}$$
⑤ \(\sqrt{6}\)
下図は，A判二枚の長方形です。
それぞれの長辺DCを重ねて並べています。A判の一つ大きいサイズの紙一枚と同様です。
例えば，A4判二枚であれば，A3判一枚と同様です。
短辺二つ分と長辺の長さを利用しています。
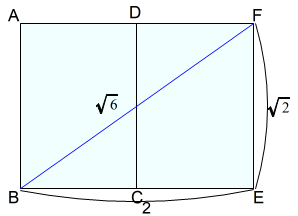$$\begin{equation}\begin{split}BE^2+EF^2&=BF^2\\2^2+\sqrt{2}^2&=BF^2\\BF^2&=6\\BF&=\sqrt{6}\end{split}\end{equation}$$
⑥ \(\sqrt{7}\)
下図では，A判三枚を使っています。
A判二枚の長辺DCを重ねて並べています。三枚目A判GEHIは，頂点Eを一致させ，A判DCEFの長辺FEにA判GEHIの対角線EIを重ねています。
短辺二つ分と対角線の長さを利用しています。
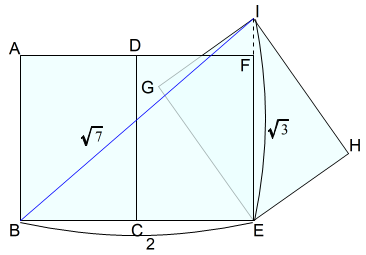
$$\begin{equation}\begin{split}BE^2+EI^2&=BI^2\\2^2+\sqrt{3}^2&=BI^2\\BI^2&=7\\BI&=\sqrt{7}\end{split}\end{equation}$$
⑦ \(\sqrt{8}\)
下図では，A判二枚を短辺DCを揃えて並べています。
\(BE\) は，長辺二つ分の長さです。
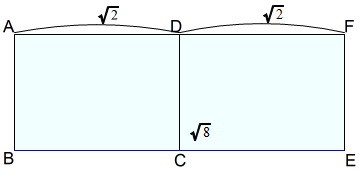
$$\begin{equation}\begin{split}BE&=BC+CE\\&=\sqrt{2}\times 2\\&=2\sqrt{2}\\&=\sqrt{8}\end{split}\end{equation}$$
⑧ \(\sqrt{9}\)
下図では，A判二枚を短辺DCを揃えて並べています。
短辺と長辺の二つ分を利用しています。
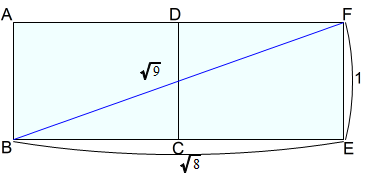
$$\begin{equation}\begin{split}BE^2+EF^2&=BF^2\\\sqrt{8}^2+1^2&=BF^2\\BF^2&=9\\BF&=\sqrt{9}=3\end{split}\end{equation}$$
⑨ \(\sqrt{10}\)
下図では，A判二枚の短辺DCを重ねています。
三枚目のA判GHEIの頂点EをA判DCEFの頂点Eと揃え，辺HEをA判DCEFの辺CEに，辺IEをA判DCEFの辺FEに重ねて配置します。
長辺二つ分と長辺一つ分の長さの組を利用しています。
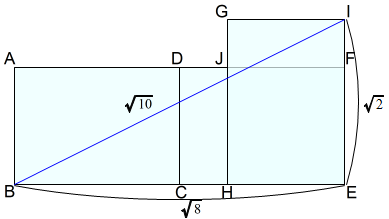
$$\begin{equation}\begin{split}BE^2+EI^2&=BI^2\\\sqrt{8}^2+\sqrt{2}^2&=BI^2\\BI^2&=10\\BI&=\sqrt{10}\end{split}\end{equation}$$
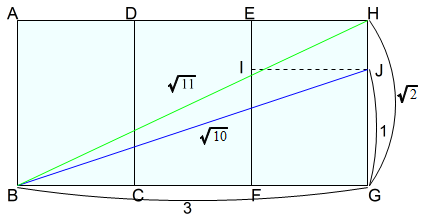
下図の場合でも\(\sqrt{10}\) ができます。
A判三枚を長辺を揃えて並べた場合です。
A判EFGHでは，\(FG=JG=FI=1\) となるよう頂点I，頂点Jをとります。
そのとき\(BJ\)が\(\sqrt{10}\) になります。短辺の三つ分と短辺一つ分（短辺を移した正方形の一辺）を利用しています。
加えて，\(BH\)は\(\sqrt{11}\)になります。
４ まとめ
A判の短辺を 1 とすると，同一番号のA判の短辺と長辺，B判の短辺と長辺の比は，次のようです。
\[1:\sqrt{2}:\sqrt{\dfrac{3}{2}}:\sqrt{3}\]
これを基にして，A判とB判の紙を工夫して並べたり折ったりすると，\(\sqrt{x},x\in X=\{2,3,4,5,6,7,8,9,10\}\)を作ることができます。
特に，A判三枚を「３ \(\sqrt{n}\)を見出す（１）A判三枚で見つかる無理数\(\sqrt{n}\)の長さ」のように配置すると，\(\sqrt{2},\sqrt{3},\sqrt{4},\sqrt{5},\sqrt{6},\sqrt{7},\sqrt{8},\sqrt{9},\sqrt{10}\)を見出すことができます。
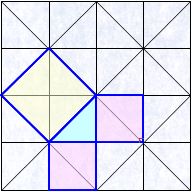
変わった形として次のような並べ方ができます。
