|
1 ソフト:小学校算数科4年「面積」導入教材ソフト
サイズ:822 KBytes ファイル名:area-intro.exe 作成者:Marche 種別:フリーソフト
確認済動作環境:WindowsVista,Windows10
2 ソフトの概要
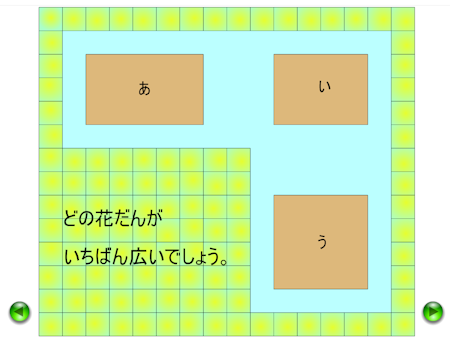
単元「面積」の導入場面の授業で,周りの長さが同じ長方形と正方形の面積を比較する問題を提示できます。
面積の意味について話し合い,問題解決につなぐことをねらいとしたシミュレーションソフトです。

3 単元の概要と指導のねらい
学習指導要領では,指導内容は以下のように示されています。
B(1)面積の単位と測定
面積について単位と測定の意味を理解し,面積を計算によって求めることができるようにする。
ア 面積の単位(平方センチメートル(cm2),平方メートル(m2),平方キロメートル(km2))について知ること。
イ 正方形及び長方形の面積の求め方を考えること。
〔算数的活動〕(1)
イ 長方形を組み合わせた図形の面積の求め方を,具体物を用いたり,言葉,数,式,図を用いたりして考え,説明する活動
ウ 身の回りにあるものの面積を実際に測定する活動
(内容の取扱い)
(5)内容の「B量と測定」の(1)のアについては,アール(a),ヘクタール(ha)の単位についても触れるものとする。
文部科学省小学校学習指導要領解説算数編平成20年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf
単元「面積」は,広さの比較や測定を通して,面積の意味をとらえます。
また,長方形や正方形の面積を単位正方形のいくつ分で求める方法を,理解できるようにすることが指導のねらいです。
① 周りの長さが等しい長方形と正方形の広さを比べる
周りの長さが等しい長方形と正方形の広さを比べる活動を設定します。
それを通して,比べようとする対象の広さは,長さという量ではないこと,周りの長さでは測れないことに気付くようにします。
このような広さと長さの違いを実感して理解できるようにします。
そして,面積は平面的な広がりをもつ量であることを具体的にイメージできるようにします。
本教材ソフトは,この導入場面で活用できます。
教師がプロジェクターで全体に提示したり,児童が個人思考の活動で考える手立てとしたりすることができます。
② 量と測定の4つの比較と測定の活動を構成する
量と測定領域の指導では,一般に,直接比較,間接比較,任意単位による測定,普遍単位による測定という学習活動を設定します。
それらを通して,量の意味や測定の単位,測定の仕方が理解できるようにします。
単元「面積」では,次のような活動を通して,児童の気付きや理解を促します。
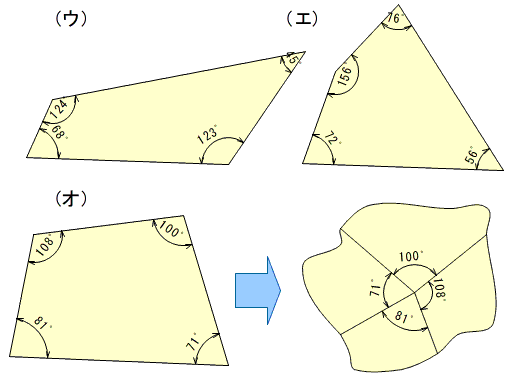
- 正方形と長方形を重ねて比べる 【直接比較】
- 正方形と長方形の形を写し取って重ねて比べる 【間接比較】(花壇のように移動できないもので問題を設定した場合は,この段階から始まる)
- 周囲にあるタイルや敷石を単位として,それが何個入るかで比べる 【任意単位による測定】
- 1辺が1cmの正方形が何個分あるかで比べる【普遍単位による測定】
1と2の活動で,児童は,比べたい量の広さが,平面的な広がりをもつ量であることに気付いてきます。
留意したいのは,1と2は「比較」,3と4は「測定」です。
単位を決めて,そのいくつ分かの数値で表すことを「測定」と言います。
量を数値で表せれば,簡単に比較できます。
測定対象である面積の意味が分かれば,その比べ方を見出せるようにします。
4 指導のポイント
(1)「長さ」の学習の見方・考え方を生かせるようにする
面積の意味を理解できるようにするためには,長さの意味や測定の仕方など,長さの学習を振り返ることが大切です。
児童は,第2学年の長さの単元で,長さや測定の意味を学ぶ単元面積と同様の流れで学習しています。
第4学年では上記の「3任意単位による測定」,「4普遍単位による測定」が中心ですが,第1学年,第2学年では「1直接比較」,「2間接比較」の経験を十分積んでいます。
そのときに学んだ見方・考え方を基にして,面積の意味や測定の仕方を類推して気付けるようにします。
そのためには,単元導入時に,長さの意味や長さの測定の意味,長さの比べ方を振り返ることが大切です。
児童が似寄りの既習の知識・技能・思考方法等を活用して問題解決するという,類推的な数学的な考え方を身に付けることは,算数科指導のねらいの一つです。
(2)長方形や正方形の面積を測定する単位は,1cmの正方形が適当であることが理解できるようにする
単位が正方形の形なら,縦置きか横置きかを考えることなく,正方形ならば回転しても大丈夫です。
正方形の形ならば,機械的に敷き詰めを考えられるよさがあります。
しかも,長さを1cmにすれば,敷き詰める単位の個数を長さと一致させられます。
長方形や正方形の辺の長さを表す数と単位正方形の個数を一致させられます。
そうすれば,長さを測ることで,並ぶ個数を見つけることができます。
例えば,単位を一辺の長さ2cmの正方形にすれば,縦4cm横6cmの長方形は,それぞれの辺の長さを2で割った数を使う必要があります。これでは不便です。
このように,児童に単位は,形が正方形,一辺の長さが1cmが適切であることを話し合わせることが大切です。
(3)公式化の際には,面積は,長さの測定と計算だけで求められるよさに気付くようにする
長方形や正方形の面積は,それぞれの辺の長さの数値が分かりさえすれば,それらの積で簡単に求められます。
長ささえ分かればよく,図形から離れて考えられます。
思考がとても楽になります。
これが算数・数学のよさのひとつです。
児童には辺の長さが分かれば積を計算するだけで簡単に面積が求められるよさに気付くようにします。
このよさは,公式のよさにもつながります。
「長方形の面積」=「縦」×「横」:面積は,長さの数値のみに依存する量なのです。
長さの数値と面積の関数関係が,そのよさの秘密です。
そして,安心して,長さの測定のみ行い計算した結果を,児童が自信をもって「これが面積です。」と言えるようにしましょう。
| 【指導のねらい】単元「面積」は,広さの比較や測定を通して,面積の意味をとらえ,長方形や正方形の面積を単位正方形のいくつ分で求める方法を理解できるようにする。
【ポイント】 |